本文链接： https://blog.csdn.net/C20190102/article/details/87557051

功能

一次FFT的功能

$O(n\log n)$ 的时间将一个多项式的系数表达式变成点值表达式（这两种表达方式后文会提到）。

一次IFFT的功能

$O(n\log n)$ 的时间将一个多项式的点值表达式变成系数表达式（这两种表达方式后文会提到）。

总体功能

$O(n\log n)$ 的时间求两个多项式的乘积。

一个 $n$ 项的整式多项式一定可以表示成： $f(x)=\sum\limits_{i=0}^{n-1}(a_ix^i)$
（有些 $a_i$ 可能为 $0$ ）

所以，一个系数 $a$ 的（有序）集合可以唯一确定一个多项式。
例如： $a=\{1,2,0,3,5\}$ 表示的就是多项式： $f(x)=1+2x+3x^3+5x^4$ 。
这里 $a=\{1,2,0,3,5\}$ 叫 $f(x)$ 的系数表达式。

所以，所谓求两个多项式的乘积，就是已知两个多项式的系数表达式，求它们乘积的多项式的系数表达式。

前置技能

（既然大家都这样说，我也这样说吧）

多项式的阶

之前说的 $f(x)=\sum\limits_{i=0}^{n-1}(a_ix^i)$ 中的 $n$ 就是它的阶，注意 $n$ 阶多项式不一定是 $n$ 次的，因为 $a_{n-1}$ 可能为 $0$ 。

多项式的系数表达式

前面已说。

多项式的点值表达式

一个 $n$ 次多项式就是一个函数，取它图像上的 $n+1$ 个不同的点就可以确定这个多项式。

例如 $f(x)$ 是个 $4$ 次多项式，取它的图像上的任意 $5$ 个不同的点： $(x_1,f(x_1))$ ， $(x_2,f(x_2))$ ，…， $(x_5,f(x_5))$ ，可以确定这个多项式的系数，因为可以列出一个 $5$ 元一次方程组解出系数。

于是一个 $n$ 次多项式的点值表达式就是它的图像上 $n+1$ 个不同的点。
换句话说， $n+1$ 个不同的点可以唯一确定一个 $n$ 次多项式。
（以上两句话式FFT和逆FFT的核心）

复数

在实数范围内，老师会告诉你负数没有平方根，所以我们为了让负数有平方根，将数的范围从实数扩展到了复数。
（实数也属于复数，复数另外一部分是虚数）

复数的基本单位

引入一个符号 $i$ ， $i^2=-1$ 。
于是任意一个复数都可以表示成 $a+bi$ ，其中 $a$ 和 $b$ 都是实数。
例如： $x^2=-7$ 的根是： $x_1=\sqrt 7i$ ， $x_2=-\sqrt 7i$ 。

复数的运算

加减乘都和整式的运算是一样的，例如两个复数 $z_1=a_1+b_1i$ ， $z_2=a_2+b_2i$ 相乘： $z_1z_2=(a_1+b_1i)(a_2+b_2i)=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i$
除法这里不会用到，但也不难，可以分母实数化：

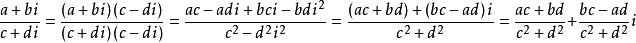
来自百度百科：复数除法

复平面

数轴可以表示一切实数，平面可以表示一切复数：

（其实这个图没有什么用）
在复平面内的一个点 $(x,y)$ 表示一个复数 $x+yi$ 。

复根

定义

定义： $\omega_n^k=cos\left(\frac{2\pi}{n}k\right)+sin\left(\frac{2\pi}{n}k\right)i$
$\omega_n^1$ 叫 $n$ 次单位复根。

很难懂是不是？把 $\omega_8^0$ ，…， $\omega_8^7$ 对应的点在复平面上画出来你就知道了。
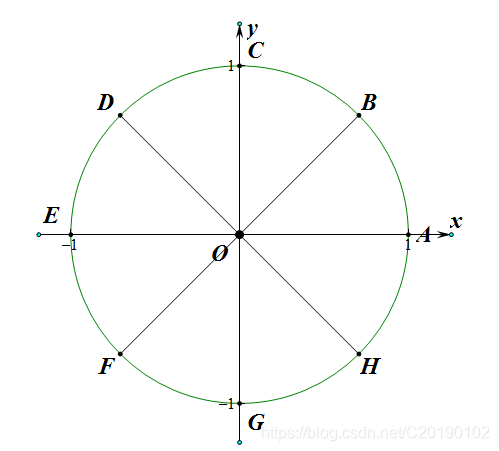
8次单位复根
（由于几何画板的公式编辑太弱，所以只标了 $ABC$ ）
点 $A$ ， $B$ ， $C$ …对应的复数分别是 $\omega_8^0$ ， $\omega_8^1$ ， $\omega_8^2$ ，…

为什么？数学必修四的单位圆与三角函数会告诉你的。

几个性质

$\omega_n^i\omega_n^j=\omega_n^{i+j}$

证明：
由于 $e^{i\theta}=cos\theta+sin\theta\cdot i$ （我不会证，貌似要用泰勒展开）
所以 $\omega_n^i=e^{\frac{2\pi}{n}i}$
所以 $\omega_n^i\omega_n^j=e^{\frac{2\pi}{n}i}e^{\frac{2\pi}{n}j}=e^{\frac{2\pi}{n}(i+j)}=\omega_n^{i+j}$

$\omega_{2n}^{2k}=\omega_n^k$
理解：它们对应的点是一样的

证明：
$\omega_{2n}^{2k}=cos\left(\frac{2\pi}{2n}2k\right)+sin\left(\frac{2\pi}{2n}2k\right)i=cos\left(\frac{2\pi}{n}k\right)+sin\left(\frac{2\pi}{n}k\right)i=\omega_n^k$

$\omega_n^{k+\frac{n}{2}}=-\omega_n^k$ （ $n$ 是偶数）
理解：它们对应的点关于原点对称。

证明： $\omega_{n}^{k+\frac{n}{2}}=cos\left(\frac{2\pi}{n}k+\pi\right)+sins\left(\frac{2\pi}{n}k+\pi\right)i=-cos\left(\frac{2\pi}{n}k\right)-sin\left(\frac{2\pi}{n}k\right)i=-\omega_n^k$

$\omega_n^{k+n}=\omega_n^k$
理解：转了一圈回到原来的点。

证明：同上一个证明

$\sum\limits_{i=0}^{n-1}(\omega_n^k)^i=0$ （ $k\neq 0$ ）（求和引理）
理解：每个点和它关于原点对称的点抵消了。

证明：
$\sum\limits_{i=0}^{n-1}(\omega_n^k)^i=1+\omega_n^k+(\omega_n^k)^2+...+(\omega_n^k)^{n-1}=\frac{(\omega_n^k)^n-1}{\omega_n^k-1}=\frac{\omega_n^{kn}-1}{\omega_n^k-1}=\frac{1-1}{\omega_n^k-1}=0$

求多项式乘积的基本步骤

已知 $k_1$ 阶多项式 $f(x)$ 和 $k_2$ 阶多项式 $g(x)$ 的系数表达式。
我们要求的是 $k_1+k_2$ 阶多项式 $h(x)=f(x)\cdot g(x)$ 的系数表达式。

统一两个多项式的阶数为 $n$ ，要保证 $n$ 是 $2$ 的幂。（系数补零即可，为什么一会说）
取 $n$ 个不同的值 $x$ ，代入 $f(x)$ 和 $g(x)$ 中，得到 $f(x)$ 和 $g(x)$ 的点值表达式： $S_{f(x)}=\{(x_1,f(x_1)),(x_2,f(x_2)),...,(x_n,f(x_n))\}$ $S_{g(x)}=\{(x_1,g(x_1)),(x_2,g(x_2)),...,(x_n,g(x_n))\}$ （两次FFT得到）
计算 $h(x)$ 的点值表达式： $S_{h(x)}=\{(x_1,f(x_1)\cdot g(x_1)),(x_2,f(x_2)\cdot g(x_2)),...,(x_n,f(x_n)\cdot g(x_n))\}$
通过 $h(x)$ 的点值表达式求 $h(x)$ 的系数表达式。
（一次IFFT得到）

忽略~~极大的~~常数，暴力的时间复杂度是 $O(n^2)$ ，FFT可以把它优化到 $O(n\log n)$ 。

FFT（IFFT）是通过计算一半的点值表达式得到另一半，要计算的那一半重复前面的步骤。

FFT

[特别提醒]

因为点值表达式中的 $x$ 集合取何值无影响，所以取算的越快的越好。
一次FFT（快速傅里叶变换）是将一个多项式的系数表达式集合变成特定（ $x$ 取 $\omega_n^0,...,\omega_n^{n-1}$ ）点值表达式中的 $y$ 集合。
一次IFFT（快速傅里叶变换逆变换）是将一个多项式的特定（ $x$ 取 $\omega_n^0,...,\omega_n^{n-1}$ ）点值表达式中的 $y$ 集合变成系数表达式集合。
注意 $n$ 是 $2$ 的幂。

递归版FFT

核心公式

我们代入求点值表达式的 $n$ 个 $x$ 是： $\omega_n^0,...,\omega_n^{n-1}$ 。

设多项式是 $A(x)=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}$
令 $A_0(x)=a_0+a_2x+a_4x^2+...+a_{n-2}x^{\frac{n}{2}-1}$
$A_1(x)=a_1+a_3x+a_5x^2+...+a_{n-1}x^{\frac{n}{2}-1}$
显然 $A(x)=A_0(x^2)+xA_1(x^2)$ （可以自己带进去算一下）

那么 $A(\omega_n^k)=A_0(\omega_n^{2k})+\omega_n^kA_1(\omega_n^{2k})=A_0(\omega_{\frac{n}{2}}^{k})+\omega_n^kA_1(\omega_{\frac{n}{2}}^{k})$
$A(\omega_n^{k+\frac{n}{2}})=A_0(\omega_n^{2k+n})+\omega_n^{k+\frac{n}{2}}A_1(\omega_n^{2k+n})=A_0(\omega_{n}^{2k})-\omega_n^kA_1(\omega_{n}^{2k})=A_0(\omega_{\frac{n}{2}}^{k})-\omega_n^kA_1(\omega_{\frac{n}{2}}^{k})$

这两个只有正负号不同！

算法流程

我们定义FFT(A,n)，表示将系数表达式的系数集合 $A$ 转换为点值表达式的 $y$ 值集合（代入的 $x$ 是 $\omega_n^0,\omega_n^1,...\omega_n^{n-1}$ ）。
那么，FFT(A,n)中，先提出 $A_0$ 和 $A_1$ ，再执行FFT(A0,n/2)和FFT(A1,n/2)。
执行完后的 $A_0$ 和 $A_1$ 已经变成了当 “ 代入的 $x$ 是 $\omega_\frac{n}{2}^0,\omega_\frac{n}{2}^1,...\omega_\frac{n}{2}^{\frac{n}{2}-1}$ ” 时，对应的 $y$ 的集合。
然后就可以循环从 $0$ 到 $\frac{n}{2}$ ，A[i]=A0[i]+w*A1[i]，A[i+n/2]=A0[i]-w*A1[i]。

代码

等讲了IFFT的递归版一起看。

非递归版FFT

算法

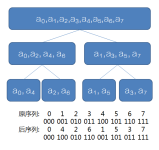
（来自不知名的大佬）

这是 $n=8$ 时的递归FFT的系数示意图。
发现最后得到的系数序列，每个数的二进制反转后恰好是最开始的序列（为什么？用心去感受一下吧）。

所以只需要把最开始的系数变成最后的样子，再一层层向上合并即可。
也就是说，把最开始的每个系数和它二进制反转后的数交换位置。

定义R[i]表示i的二进制反转后的数，L是i的二进制位数（即 $\log_2 n$ ），那么有：
R[i]=(R[i>>1]>>1)|((i&1)<<(L-1))

下面是解释：
R[i>>1]表示i除去最后一位后前面几位的反转，那么把它和i的最后一位换个位置就好了。

代码

等讲了IFFT的非递归版一起看。

IFFT

FFT的矩阵表达

$\left( \begin{matrix} y_0\\ \\ y_1\\ \\ y_2\\ \\ y_3\\ \\ \vdots\\ \\ y_{n-1} \end{matrix} \right)= \left( \begin{matrix} \omega_n^0 & \omega_n^0 & \omega_n^0 & \omega_n^0 & \cdots & \omega_n^0\\ \\ \omega_n^0 & \omega_n^1 & \omega_n^2 & \omega_n^3 & \cdots & \omega_n^{n-1}\\ \\ \omega_n^0 & \omega_n^2 & \omega_n^4 & \omega_n^6 & \cdots & \omega_n^{2(n-1)}\\ \\ \omega_n^0 & \omega_n^3 & \omega_n^6 & \omega_n^9 & \cdots & \omega_n^{3(n-1)}\\ \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ \\ \omega_n^0 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \omega_n^{3(n-1)} & \cdots & \omega_n^{(n-1)(n-1)}\\ \end{matrix} \right)\times\\ \left( \begin{matrix} a_0\\ \\ a_1\\ \\ a_2\\ \\ a_3\\ \\ \vdots\\ \\ a_{n-1} \end{matrix} \right)$

FFT可以表示为这样， $\{y\}$ 是点值表达式的 $y$ 值集合， $\{a\}$ 是系数表达式的系数集合。
（矩阵乘法可以自己百度一下，在这里就是 $y_k=\sum\limits_{i=0}^{n-1}\left(a_i\omega_n^{ki}\right)$ ）

例如： $y_2=f(x_2)=f(\omega_n^2)=a_0(\omega_n^2)^0+a_1(\omega_n^2)^1+a_2(\omega_n^2)^2+...+a_{n-1}(\omega_n^2)^{n-1}$ $=a_0\omega_n^0+a_1\omega_n^2+a_2\omega_n^4+...+a_{n-1}\omega_n^{2(n-1)}$ $=\sum\limits_{i=0}^{n-1}\left(a_i\omega_n^{2i}\right)$

IFFT的矩阵表达

令 $V=\left( \begin{matrix} \omega_n^0 & \omega_n^0 & \omega_n^0 & \omega_n^0 & \cdots & \omega_n^0\\ \\ \omega_n^0 & \omega_n^1 & \omega_n^2 & \omega_n^3 & \cdots & \omega_n^{n-1}\\ \\ \omega_n^0 & \omega_n^2 & \omega_n^4 & \omega_n^6 & \cdots & \omega_n^{2(n-1)}\\ \\ \omega_n^0 & \omega_n^3 & \omega_n^6 & \omega_n^9 & \cdots & \omega_n^{3(n-1)}\\ \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ \\ \omega_n^0 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \omega_n^{3(n-1)} & \cdots & \omega_n^{(n-1)(n-1)}\\ \end{matrix} \right)$
则 $\left( \begin{matrix} y_0\\ \\ y_1\\ \\ y_2\\ \\ y_3\\ \\ \vdots\\ \\ y_{n-1} \end{matrix} \right)= V\times\\ \left( \begin{matrix} a_0\\ \\ a_1\\ \\ a_2\\ \\ a_3\\ \\ \vdots\\ \\ a_{n-1} \end{matrix} \right)$
那么 $\left( \begin{matrix} y_0\\ \\ y_1\\ \\ y_2\\ \\ y_3\\ \\ \vdots\\ \\ y_{n-1} \end{matrix} \right)\times V^{-1}= \left( \begin{matrix} a_0\\ \\ a_1\\ \\ a_2\\ \\ a_3\\ \\ \vdots\\ \\ a_{n-1} \end{matrix} \right)$

也就是说，我们只要构造出 $V^{-1}$ ，IFFT就解决了。

换句话说，要构造一个矩阵 $V^{-1}$ ，使得 $V\times V^{-1}=A$ （ $A$ 是单位矩阵）
其中 $A= \left( \begin{matrix} 1 & 0 & 0 & \cdots & 0\\ 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & 1 \end{matrix} \right)$

（计算一下会发现任何矩阵乘 $A$ 都是它本身）

于是傅里叶说，
$V^{-1}= \left( \begin{matrix} \frac{1}{n}\omega_n^0 & \frac{1}{n}\omega_n^0 & \frac{1}{n}\omega_n^0 & \frac{1}{n}\omega_n^0 & \cdots & \frac{1}{n}\omega_n^0\\ \\ \frac{1}{n}\omega_n^0 & \frac{1}{n}\omega_n^{-1} & \frac{1}{n}\omega_n^{-2} & \frac{1}{n}\omega_n^{-3} & \cdots & \frac{1}{n}\omega_n^{-(n-1)}\\ \\ \frac{1}{n}\omega_n^0 & \frac{1}{n}\omega_n^{-2} & \frac{1}{n}\omega_n^{-4} & \frac{1}{n}\omega_n^{-6} & \cdots & \frac{1}{n}\omega_n^{-2(n-1)}\\ \\ \frac{1}{n}\omega_n^0 & \frac{1}{n}\omega_n^{-3} & \frac{1}{n}\omega_n^{-6} & \frac{1}{n}\omega_n^{-9} & \cdots & \frac{1}{n}\omega_n^{-3(n-1)}\\ \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ \\ \frac{1}{n}\omega_n^0 & \frac{1}{n}\omega_n^{-(n-1)} & \frac{1}{n}\omega_n^{-2(n-1)} & \frac{1}{n}\omega_n^{-3(n-1)} & \cdots & \frac{1}{n}\omega_n^{-(n-1)(n-1)}\\ \end{matrix} \right)$

简单点说，（下标从零开始） $V_{i,j}=\omega_n^{ij}$ ， $V^{-1}{}_{i,j}=\frac{1}{n}\omega_n^{-ij}$ 。

接下来要证明 $V\times V^{-1}=A=\left( \begin{matrix} 1 & 0 & 0 & \cdots & 0\\ 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & 1 \end{matrix} \right)$

根据矩阵乘法的定义， $A_{x,y}=\sum\limits_{i=0}^{n-1}(V_{x,i}V^{-1}{}_{i,y})$ $=\sum\limits_{i=0}^{n-1}\left(\omega_n^{xi}\frac{1}{n}\omega_n^{-iy}\right)$ $=\frac{1}{n}\sum\limits_{i=0}^{n-1}(\omega_n^{x-y})^i$

当 $x=y$ 时， $\omega_n^{x-y}=1$ ， $A_{i,j}=1$ ；
当 $x\neq y$ 时，根据求和引理， $A_{i,j}=0$ 。

得证。

综上所述：

FFT
$\left( \begin{matrix} y_0\\ \\ y_1\\ \\ y_2\\ \\ y_3\\ \\ \vdots\\ \\ y_{n-1} \end{matrix} \right)= \left( \begin{matrix} a_0\\ \\ a_1\\ \\ a_2\\ \\ a_3\\ \\ \vdots\\ \\ a_{n-1} \end{matrix} \right)\times\\ \left( \begin{matrix} \omega_n^0 & \omega_n^0 & \omega_n^0 & \omega_n^0 & \cdots & \omega_n^0\\ \\ \omega_n^0 & \omega_n^1 & \omega_n^2 & \omega_n^3 & \cdots & \omega_n^{n-1}\\ \\ \omega_n^0 & \omega_n^2 & \omega_n^4 & \omega_n^6 & \cdots & \omega_n^{2(n-1)}\\ \\ \omega_n^0 & \omega_n^3 & \omega_n^6 & \omega_n^9 & \cdots & \omega_n^{3(n-1)}\\ \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ \\ \omega_n^0 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \omega_n^{3(n-1)} & \cdots & \omega_n^{(n-1)(n-1)}\\ \end{matrix} \right)$
IFFT
$\left( \begin{matrix} a_0\\ \\ a_1\\ \\ a_2\\ \\ a_3\\ \\ \vdots\\ \\ a_{n-1} \end{matrix} \right)= \left( \begin{matrix} y_0\\ \\ y_1\\ \\ y_2\\ \\ y_3\\ \\ \vdots\\ \\ y_{n-1} \end{matrix} \right)\times\left( \begin{matrix} \frac{1}{n}\omega_n^0 & \frac{1}{n}\omega_n^0 & \frac{1}{n}\omega_n^0 & \frac{1}{n}\omega_n^0 & \cdots & \frac{1}{n}\omega_n^0\\ \\ \frac{1}{n}\omega_n^0 & \frac{1}{n}\omega_n^{-1} & \frac{1}{n}\omega_n^{-2} & \frac{1}{n}\omega_n^{-3} & \cdots & \frac{1}{n}\omega_n^{-(n-1)}\\ \\ \frac{1}{n}\omega_n^0 & \frac{1}{n}\omega_n^{-2} & \frac{1}{n}\omega_n^{-4} & \frac{1}{n}\omega_n^{-6} & \cdots & \frac{1}{n}\omega_n^{-2(n-1)}\\ \\ \frac{1}{n}\omega_n^0 & \frac{1}{n}\omega_n^{-3} & \frac{1}{n}\omega_n^{-6} & \frac{1}{n}\omega_n^{-9} & \cdots & \frac{1}{n}\omega_n^{-3(n-1)}\\ \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots\\ \\ \frac{1}{n}\omega_n^0 & \frac{1}{n}\omega_n^{-(n-1)} & \frac{1}{n}\omega_n^{-2(n-1)} & \frac{1}{n}\omega_n^{-3(n-1)} & \cdots & \frac{1}{n}\omega_n^{-(n-1)(n-1)}\\ \end{matrix} \right)$

算法流程

既然构造出来了 $V^{-1}$ ，我们就知道要代入计算的 $x$ 集合就是：
$\{\omega_n^0,\omega_n^{-1},...,\omega_n^{-(n-1)}\}$

为了减少误差，最后统一乘 $\frac{1}{n}$ 。

把 “ 求多项式乘积的基本步骤 ” 中的第3步得到的 $h(x)$ 的点值表达式的 $y$ 集合当做一个多项式的系数表达式集合，用一次FFT求出 $x$ 集合是 $\{\omega_n^0,\omega_n^{-1},...,\omega_n^{-(n-1)}\}$ 时，这个多项式的点值表达式的 $y$ 集合，就是 $h(x)$ 的系数集合的 $n$ 倍。

还记得FFT算法流程的这一步吗：
A[i]=A0[i]+w*A1[i]，A[i+n/2]=A0[i]-w*A1[i]

将它变为这样就是IFFT了：
A[i]=A0[i]-w*A1[i]，A[i+n/2]=A0[i]+w*A1[i]

现在知道为什么代码要一起展示了，因为只需在FFT函数中加一个参数就可以实现逆变换了。

代码

看下面。

代码

大整数乘法一般的时间复杂度是 $O(n^2)$ ，把两个大整数看成两个多项式的系数，求它们的乘积，最后处理进位，就可以做到 $O(n\log n)$ 了。

递归版

据说递归版要爆空间（我这道题和洛谷上的那道都用递归的过了），所以大家都写非递归版。

#include<cmath>
#include<cstdio>
#include<cstring>

#define LOG 17
#define MAXN (1<<LOG)
int res[MAXN+5];
char x[MAXN+5],y[MAXN+5];

struct Complex{
    double x,y;//x+yi
    Complex(){x=y=0;}
    Complex(double a,double b):x(a),y(b){}
    Complex operator + (Complex b)const{return Complex(x+b.x,y+b.y);}
    Complex operator - (Complex b)const{return Complex(x-b.x,y-b.y);}
    Complex operator * (Complex b)const{return Complex(x*b.x-y*b.y,y*b.x+x*b.y);}
}A0[MAXN+5],B0[MAXN+5];
//复数类，好像C++有一个叫complex的库

#define PI acos(-1)
void FFT(Complex *A,int len,int sign){
    if(len==1)
        return;
    int mid=len>>1;
    Complex A1[mid+5],A2[mid+5];//按奇偶分离系数到A1和A2
    for(int i=0;i<mid;i++)
        A1[i]=A[i<<1],A2[i]=A[i<<1|1];
    FFT(A1,mid,sign),FFT(A2,mid,sign);
    for(int i=0;i<mid;i++){
        Complex w(cos(2.0*PI/len*i),sign*sin(2.0*PI/len*i));
        //w是len次单位复根的i次方
        //sign=-1是逆变换
        A[i]=A1[i]+w*A2[i],A[i+mid]=A1[i]-w*A2[i];
    }
}

int main(){
    while(~scanf("%s%s",x+1,y+1)){
        int len1=strlen(x+1),len2=strlen(y+1),N=1;
        while(N<len1+len2)
            N<<=1;
        //统一长度为2的幂
        for(int i=0;i<len1;i++)
            A0[i]=Complex(x[len1-i]-'0',0);
        for(int i=0;i<len2;i++)
            B0[i]=Complex(y[len2-i]-'0',0);
        //倒着存可以避免很多恶心的问题
        FFT(A0,N,1);
        FFT(B0,N,1);
        for(int i=0;i<N;i++)
            A0[i]=A0[i]*B0[i];
        //得到乘积多项式的点值表达式
        FFT(A0,N,-1);
        for(int i=0;i<N;i++)
            res[i+1]=int(A0[i].x/N+0.5);
        //注意最后统一除以n，为避免精度误差，+0.5再取整
        for(int i=1;i<=N;i++)
            res[i+1]+=res[i]/10,res[i]%=10;
        while(N>1&&res[N]==0)
            N--;
        //处理进位和前导零
        for(int i=N;i>=1;i--)
            putchar(res[i]+'0');
        putchar('\n');
        memset(A0,0,sizeof A0);
        memset(B0,0,sizeof B0);
        memset(res,0,sizeof res);
    }
}

非递归版

建议写这种。

#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

#define LOG 17
#define MAXN (1<<LOG)
int res[MAXN+5];
char x[MAXN+5],y[MAXN+5];

struct Complex{
    double x,y;//x+yi
    Complex(){x=y=0;}
    Complex(double a,double b):x(a),y(b){}
    Complex operator + (Complex b)const{return Complex(x+b.x,y+b.y);}
    Complex operator - (Complex b)const{return Complex(x-b.x,y-b.y);}
    Complex operator * (Complex b)const{return Complex(x*b.x-y*b.y,y*b.x+x*b.y);}
}A0[MAXN+5],B0[MAXN+5];

#define PI acos(-1)
int R[MAXN+5];
void FFT(Complex *A,int len,int sign){
    for(int i=0;i<len;i++)
        if(i<R[i])//不加的话会swap两次，最后什么都没有发生
            swap(A[i],A[R[i]]);
    //调整成最后的顺序
    for(int mid=1;mid<len;mid<<=1)//枚举当前要处理的区间长度的一半
        for(int i=0;i<len;i+=mid<<1)//每2*mid的长度为一段，分开处理
            for(int j=0;j<mid;j++){//处理当前2*mid长度的区间
                Complex w(cos(PI/mid*j),sign*sin(PI/mid*j));//2.0被mid消掉了
                Complex tmp1=A[i+j],tmp2=A[i+j+mid];
                A[i+j]=tmp1+w*tmp2;
                A[i+j+mid]=tmp1-w*tmp2;
            }
}

int main(){
    while(~scanf("%s%s",x+1,y+1)){
        int len1=strlen(x+1),len2=strlen(y+1),N=1,Log=0;
        while(N<len1+len2)
            N<<=1,Log++;
        for(int i=0;i<len1;i++)
            A0[i]=Complex(x[len1-i]-'0',0);
        for(int i=0;i<len2;i++)
            B0[i]=Complex(y[len2-i]-'0',0);
        for(int i=0;i<N;i++)
            R[i]=(R[i>>1]>>1)|((i&1)<<(Log-1));
        //dp得到R数组
        FFT(A0,N,1),FFT(B0,N,1);
        for(int i=0;i<N;i++)
            A0[i]=A0[i]*B0[i];
        FFT(A0,N,-1);
        for(int i=0;i<N;i++)
            res[i+1]=int(A0[i].x/N+0.5);
        for(int i=1;i<=N;i++)
            res[i+1]+=res[i]/10,res[i]%=10;
        while(N>1&&res[N]==0)
            N--;
        for(int i=N;i>=1;i--)
            putchar(res[i]+'0');
        putchar('\n');
        memset(A0,0,sizeof A0);
        memset(B0,0,sizeof B0);
        memset(res,0,sizeof res);
    }
}

后记

感谢这些大佬：

CXH大佬
 十分简明易懂的FFT（快速傅里叶变换）
小学生都能看懂的FFT！！！
快速傅里叶变换(FFT)详解

FFT（快速傅里叶变换）算法

文章目录

功能

一次FFT的功能

一次IFFT的功能

总体功能

前置技能

多项式的阶

多项式的系数表达式

多项式的点值表达式

复数

复数的基本单位

复数的运算

复平面

复根

定义

几个性质

求多项式乘积的基本步骤

FFT

递归版FFT

核心公式

算法流程

代码

非递归版FFT

算法

代码

IFFT

FFT的矩阵表达

IFFT的矩阵表达

算法流程

代码

代码

递归版

非递归版

后记

猜你喜欢