快速傅里叶变换（FFT）

多项式的概念

1. 多项式次数界：

关于x的多项式即形如 $f(x)=a_0+a_1x+a_2x^1+\dots+a_nx^n$ 的式子，其中最高项的次数为 $n$ ，则任何大于 $n$ 的整数都成为该多项式的次数界，但一般我们取最小的次数界，即该多项式的次数界为 $n+1$ 。所以一个次数界为 $n$ 的多项式，它的最高项次数为 $n-1$ .

2.多项式的两种表示方法：

系数表示法：
一个次数界为n的多项式，最多有n个系数，如果确定了这n个系数，则多项式可以唯一确定。
点值表示法：
如果给出了 $n$ 不同的的 $x$ 值，并对应的给出了 $n$ 个 $f(x)$ 值，则次数界为 $n$ 的多项式也可以唯一确定，所以我们也可以用 $n$ 对 $(x,f(x))$ 的点值，唯一地确定多项式。

3.多项式的运算

若有 $f(x)=a_0+a_1x+a_2x^2+\dots+a_nx^n$ , $g(x)=b_0+b_1x+b_2x^2+\dots+b_nx^n$ ，我们来讨论一下多项式的运算。
多项式的加减
$f(x)\pm g(x)=(a_0 \pm b_0)+(a_1\pm b_1)x+(a_2 \pm b_2)x^2+\dots+(a_n\pm b_n)x^n$ .
一次加减操作是O(n)的。
而如果是点值表示法，我们需要对n个点值进行加减，所以也是 $O(n)$ 的。
多项式的乘法
如果是系数表示法，很明显是 $O(n^2)$ 的。
如果是点值表示法，因为最高项变成了2n-2次，所以我们需要2n-1对x和f(x)值才能唯一确定。这一过程仍然是 $O(n)$ 的。
对于两个多项式的系数表示的乘法运算，我们能否先把他们转换为点值表示法，然后进行乘法运算，然后再把结果转换为系数表示法呢？
我们先来看一下系数表示法和点值表示法互换的时间复杂度。
已知系数表示法，求一个点的f(x)，可以使用秦九韶算法，在O(n)时间内求出来。
$f(x_0)=a_0+x(a_1+x(a_2+x(a_3+x(\dots+x(a_{n-1}+xa_n))\dots)$
于是将一个多项式从系数表示法换成点值表示法需要 $O(n^2)$ .
那么反过来，将一个多项式从点值表示法换成系数表示法呢？
似乎更高！使用高斯消元，需要 $O(n^3)$ 的时间复杂度。
有没有什么办法优化？
忘了介绍了，从系数表示法转换为点值表示法，我们称这一过程为求值；从点值表示法换成系数表示法，这一过程我们称之为插值。
使用拉格朗日插值法，我们可以将插值的时间复杂度稍微降低一点，
$f(x)=\sum_{1 \leq i \leq n} y_i\prod_{1 \leq j \leq n \land j \neq i} \frac{x-x_j}{x_i-x_j}$
考虑到有很多重复的计算，看分子，我们可以预处理出 $\omega(x)=\prod_{1\leq j \leq n}(x-x_j)$

$l_i=\prod_{1\leq j \leq n \land j \neq i}\frac{y_i}{x_i-x_j}$
则可得：
$f(x)=\omega(x)\sum_{1\leq i \leq n} \frac{l_i}{x-x_i}$
时间复杂度降为 $O(n^2)$
然而时间复杂度还是没法优化，仍然为 $O(n^2)$ .

4.快速傅里叶变换

我们可以精心地选择n个x的值，使得求值和插值均能够利用分治，从而达到 $O(NlogN)$ 的时间复杂度。
(一). 单位复数根
先了解一下复数。复数包含实部和虚部。
如果把实部看做x轴，虚部看做y轴，则可以得到复平面。
则复平面上的任意点都表示一个复数。
对于一个最高项次数为n的方程，如: $f(x)=a_nx^n+a_{n-1}x^{n-1}+\dots+a_1x+a_0=0$ ,如果考虑复数根，它一定有n个。

满足 $x^n=1$ 的n个解，称为单位复数根。n次单位复根刚好有n个,这些根为
$e^{2\pi ik/n}$ .我们利用了复数的指数形式的定义.
$e^{i \omega}=cos(\omega)+isin(\omega)$
由此可见,这n个复根在复平面上是均匀分布在以原点为圆心的单位半径的圆周上.而其中 $\omega_n=e^{2\pi i/n}$ ,称为主n次单位根,所有其他的n次单位复根都是 $\omega_n$ 的幂.
单位复数根具备这样的性质:
(1).消去引理:对任何整数 $n\geq 0,k\geq 0$ ,以及 $d \gt 0$ ,有 $\omega_{dn}^{dk}=\omega_n^k$ .
(2).折半引理:如果 $n>0$ 为偶数,那么n个n次单位复根的平方的集合就是n/2个n/2次单位复数根的集合.
利用消去引理即可证明.
(3).求和引理对于任意整数 $n\geq 1$ 和不能被n整除的非负整数k,有
$\sum_{j=0}^{n-1}(\omega_n^k)^j=0$

(二).DFT
对于次数界为n的多项式, $A(x)=\sum_{j=0}^{n-1}a_jx^j$
在 $\omega_n^0,\omega_n^1,\omega_n^2,\dots,\omega_n^{n-1}$ 处求值,得到向量 $y=(y_0,y_1,\dots,y_{n-1})$ ,则称y为系数向量 $a=(a_0,a_1,\dots,a_{n-1})$ 的离散傅里叶变换(DFT).记为 $y=DFT_n(a)$
(三).FFT
这是一种算法,可以在 $O(NlogN)$ 的时间复杂度类计算出 $DFT_n(a)$ .它主要基于分治的策略。
设
$A^{[0]}(x)=a_0+a_2x^1+\dots+a_{n-2}x^{n/2-1}$
$A^{[1]}(x)=a_1x+a_3x^1+\dots+a_{n-1}x^{n/2-1}$
则 $A(x)=A^{[0]}(x^2)+xA^{[1]}(x^2)$ .
则A(x)在 $\omega_n^1,\omega_n^2,\omega_n^3,\dots,\omega_n^{n-1}$ 处的问题则转换为:
求次数界为n/2的多项式 $A^{[0]}(x)$ 和 $A^{[1]}(x)$ 在 $\omega_{n/2}^0,\omega_{n/2}^1,\dots,\omega_{n/2}^{n/2-1}$ 处的值.
这里要求n为2的幂,这样才能保证 $\omega_n^{2i}=\omega_{n/2}^i$ .

//递归写法，用于理解FFT。因为有更好的迭代写法，这种写法一般不用。
int *fft(int a[],int len)  //len is a power of 2
{ 
	if(len==1)
	return a;
	complex wn(cos(2*Pi/n),sin(2*Pi/n));
	complex w(1,0);
	static int a1[len/2+1],a2[len/2+1];
	static int y[len];
	for(int i=0;i<n/2;i++)
	{
	   a1[i]=a[i*2];
	   a2[i]=a[2*i+1]);
	}
	int *y0=fft(a1,n/2);
	int* y1=fft(a2,n/2);
	for(int i=0;i<n/2;i++)
	{
	y[i]=y0[i]+y1[i]*w;
	y[i+n/2]=y0-y1*w;
	w=w*wn;
	}
	return y;
}

我们于是完成了对次数界为n的多项式在n次单位复根处的求值,从而得到它的点值表示法.这里的时间复杂度是O(NlogN)的.
接下来,我们可以通过点值表示法完成两个多项式的乘积,时间复杂度仍然是O(N)的.
然后,我们要把乘积的点值表示法换成系数表示法,这个过程是求值的逆运算,称为插值.
求值运算是这样的:
$\left(\begin{array}{c} 1& 1 & 1 & \dots &1 \\ 1& \omega_{n}^1 & \omega_n^2 & \dots & \omega_n^{n-1} \\ 1 & \omega_n^2 & \omega_n^4 & \dots & \omega_n^{2(n-1)} \\ \vdots & \vdots & \vdots &\vdots & \vdots \\ 1 & \omega_n^{n-1} & \omega_n^{2(n-1)} & \dots & \omega_n^{(n-1)(n-1)} \end{array}\right) \left(\begin{array}{c} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_n \end{array} \right)=\left(\begin{array}{c} y_0 \\ y_1 \\ y_2 \\ \vdots \\ y_{n-1} \end{array} \right)$

左边的矩阵是范德蒙德矩阵, $[V]_{ij}=\omega_n^{ij}$ ,可以构造出它的逆矩阵 $V^{-1}$ ,其中 $[V^{-1}]_{ji}=1/n \omega_n^{-ij}$ .
于是可以得到插值的运算是这样的:
$\left(\begin{array}{c} 1/n& 1/n & 1/n & \dots &1/n \\ 1/n &\omega_{n}^{-1}/n & \omega_n^{-2}/n & \dots & \omega_n^{-(n-1)} \\ 1/n & \omega_n^{-2}/n &\omega_n^{-4}/n & \dots & \omega_n^{-2(n-1)}/n \\ \vdots & \vdots & \vdots &\vdots & \vdots \\ 1/n & \omega_n^{-(n-1)}/n & \omega_n^{-2(n-1)}/n & \dots & \omega_n^{-(n-1)(n-1)}/n \end{array}\right) \left(\begin{array}{c} y_0 \\ y_1\\y_2 \\ \vdots \\ y_{n-1} \end{array} \right)=\left(\begin{array}{c} a_0 \\ a_1 \\a_2 \\ \vdots \\ a_n \end{array} \right)$
我们只需要在求值运算的基础上,稍作一些变换,将 $a_n$ 和 $y_n$ 互换,用 $\omega_n^{-1}$ 代替 $\omega_n$ ,并将计算结果中每一项除以n即可.
于是,我们也可以在 $O(NlogN)$ 时间内求出 $DFT_n^{-1}$ .

(四).FFT的高效算法
上面的算法是递归的,我们可以把它改成迭代的.
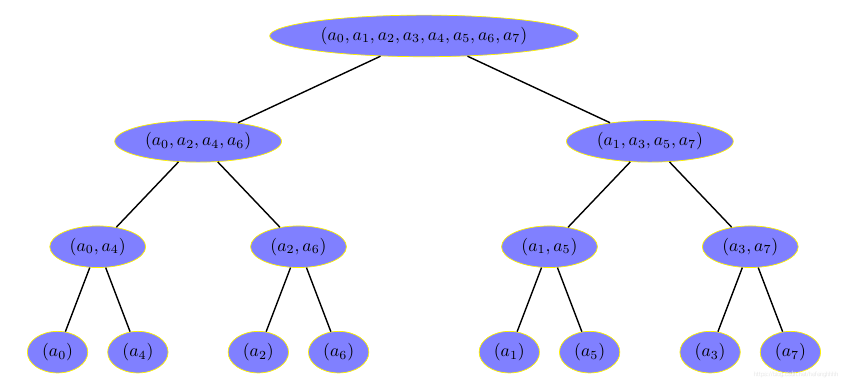
观察向量 $A=\{a_0,a_1,\dots,a_n\}$ ,它每次都是按照奇偶分成两个向量 $A^{[0]}$ 和 $A^{[1]}$ .

FFT的系数变化规律
观察最底层系数的排列顺序,如果看他们的二进制,发现刚好0~7的二进制翻转,即镜面效果.为什么有这样的规律呢?
稍微一想,就能明白,因为我们是按照奇偶性来分的,就是按照最低位为0或为1来分的.所以排在前面的一半都是最低位为0的,后面的一般是最低位为1的.在每一半里,又是次低位为0的排前面,次低位为1 的排后面.如果把最低位看做最高位,次低位看做次高位,即将每个数镜面翻转,则它就是按照递增顺序排列的.也就是说,对于任何一个系数,如何它的编号是高低位镜面对称的,则它位置不变,否则,必然存在另一个系数,编号与它的编号镜面对称,则这两个数需要交换位置.这个置换我们称为位逆序置换,代码如下:

void change(complex num[],int len)
    {
        for(int i=1,j=len/2;i<len-1;i++)
        {
            if(i<j)swap(num[i],num[j]);
            int k=len/2;
            while(j>=k)
            {
                j-=k;
                k/=2;
            }
            if(j<k)
            j+=k;
        }
    }

接下来看一个简单的模板题:求a×b的结果。
其中a、b最多不超过50000位。
将a，b看做多项式f(x)和g(x),a*b即是将f(x)与g(x)两个多项式计算卷积，然后再令x=10的结果。
于是可以使用FFT。
注意不要压位太狠，系数有可能爆int。下面的代码没有压位。且保持读入的高低位顺序，即a1、a2数组从左到右即为读入的两个高精度数从高到低的顺序。

代码：
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
using namespace std;
#define MAXN 200005
#define LL int
#define max(a,b) (a>b?a:b)
LL num1[MAXN],num2[MAXN],ans[MAXN];
char s1[MAXN],s2[MAXN];
int len1,len2,n;
const double PI=acos(-1.0);
struct complex
{
    double r,i;
    complex(double _r=0,double _i=0):r(_r),i(_i){}
    complex operator +(const complex &t)const
    {
        return complex(r+t.r,i+t.i);
    }
    complex operator -(const complex &t)const
    {
        return complex(r-t.r,i-t.i);
    }
    complex operator *(const complex &t)const
    {
        return complex(r*t.r-i*t.i,r*t.i+i*t.r);
    }
}a1[MAXN],a2[MAXN],w,wn;
void change(complex num[],int len)
    {
        for(int i=1,j=len/2;i<len-1;i++)
        {
            if(i<j)swap(num[i],num[j]);
            int k=len/2;
            while(j>=k)
            {

                j-=k;
                k/=2;
            }
            if(j<k)
            j+=k;
        }
    }
void fft(complex num[],int len,int flg)
    {
        for(int i=2;i<=len;i<<=1)
        {
            wn=complex(cos(flg*2*PI/i),sin(flg*2*PI/i));
            for(int j=0;j<len;j+=i)
            {
                w=complex(1,0);
                for(int k=j;k<j+i/2;k++)
                {
                    complex u=w*num[k+i/2];
                    complex t=num[k];
                    num[k]=t+u;
                    num[k+i/2]=t-u;
                    w=w*wn;
                }
 
            }
        }
        if(flg==-1)
        for(int i=0;i<len;i++)
        num[i].r/=len;
    }
int main()
{
    while(~scanf("%s %s",s1,s2))
    {
        memset(ans,0,sizeof ans);
        memset(a1,0,sizeof a1);
        memset(a2,0,sizeof a2);
        len1=strlen(s1);
        len2=strlen(s2);
        int len=len1+len2;
        n=1;
        while(n<len)n<<=1;
        for(int i=0;i<len1;i++)
        a1[i]=complex((double)(s1[i]-'0'),0);
        for(int i=len1;i<n;i++)
        a1[i]=complex(0,0);
        for(int i=0;i<len2;i++)
        a2[i]=complex((double)(s2[i]-'0'),0);
        for(int i=len2;i<n;i++)
        a2[i]=complex(0,0);
        change(a1,n);
        change(a2,n);
        fft(a1,n,1);
        fft(a2,n,1);
        for(int i=0;i<n;i++)
        a2[i]=a1[i]*a2[i];
        change(a2,n);
        fft(a2,n,-1);
        for(int i=0;i<len1+len2-1;i++)
        ans[i]=(LL)(a2[i].r+0.5);
        for(int i=len1+len2-2;i>0;i--)
        {
            ans[i-1]+=ans[i]/10;
            ans[i]%=10;
        }
        int ii;
       for(ii=0;ans[ii]==0&&ii<len1+len2-1;ii++);
        if(ii==len1+len2-1)printf("0");
        else
       while(ii<len1+len2-1)
        {printf("%d",ans[ii]);
         ii++;
        }
       
         printf("\n");
      }
    return 0;
}