快速傅里叶变换（FFT）（学习笔记）

其他 2018-12-02 21:30:02 阅读次数: 0
版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/sizeof_you/article/details/84336752

学习了一波 F F T FFT ，只是浅浅的入门。还有很多前置知识，有一些还不是太了解，完了深入学习之后再补博客 q w q qwq
以下内容大部分参考秦岳学长的课件

多项式

形如 A ( x ) = ∑ k = 0 n − 1 a k × x k A(x)=\sum_{k=0}^{n-1}a_k\times x^k ，其中 a k a_k 为多项式系数
C ( x ) = A ( x ) + B ( x ) C(x)=A(x)+B(x) ： c k = a k + b k c_k=a_k+b_k
C ( x ) / A ( x ) = B ( x ) C(x)/A(x)=B(x) ： c n = ∑ a k × b n − k c_n=\sum a_k\times b_{n-k}

多项式的表示法：
系数表达式：上面说的
点值表达式：给出 N + 1 N+1 个不同的 x x 代入 A ( x ) A(x) 的点值，这样的 N + 1 N+1 个元素构成的集合 { ( x 0 , y 0 ) , ( x 1 , y 1 ) , … , ( x n , y n ) } \{(x0,y0),(x1,y1),…,(xn,yn)\} ，其中 y i y_i = A ( x i ) A(x_i) ，称为点值表示法。

唯一性定理：证明可用范德蒙矩阵行列式

系数与点值：
系数表示法的 n n 次多项式 A ( x ) , B ( x ) A(x),B(x) 可以 O ( n ) O(n) 快速求得 A ( x ) + B ( x ) A(x)+B(x) ，但是卷积通常需要 O ( n 2 ) O(n^2) 计算

点值表示法的 n n 次多项式卷积也可以 O ( n ) O(n) 计算，只需将值域 y y 对应相乘即可 { ( x i , y i ) } × { ( x i , z i ) } = { ( x i , y i ∗ z i ) } \{(xi,yi)\}×\{(xi,zi)\}=\{(xi,yi*zi)\} (由于 n n 项确定次数界为 n n 的多项式，故计算卷积是至少保留 2 n 2n 项)

实际上点值表示法的卷积计算的是圆周卷积

点值与系数的转化：
1. 1. 系数表示法 → → 点值表示法
朴素计算 O ( n 3 ) O(n^3)
秦九韶算法/霍纳法则 O ( n 2 ) O(n^2)
2. 2. 点值表示法 → → 系数表示法
高斯消元 O ( n 3 ) O(n^3)
拉格朗日插值法 O ( n 2 ) O(n^2) ： A ( x ) = ∑ 0 < = k < = n y k ∗ Π ( j ≠ k ) ( x − x j ) / ( x k − x j ) A(x)=∑_{0<=k<=n}y_k*Π(j≠k)(x-x_j)/(x_k-x_j)
(原理:构造求和式当 x = x k x=x_k 时只有一项为 y k y_k ，其余全为 0 0 )

(霍纳法则不会 q w q qwq ，等以后补

而 F F T FFT 可以在 O ( n l o g n ) O(nlogn) 时间内求出多项式卷积

复数

单位复数 i = s q r t ( − 1 ) i=sqrt(-1) ，复数表示为 ( a + b × i ) (a+b\times i) 的形式，运算和实数类似。
其实复数就相当于向量，复数的计算可以用向量计算来解决

struct complex{
    double x,y;
    complex(double xx=0,double yy=0) {x=xx,y=yy;}
}a[maxn],b[maxn];
complex operator +(complex a,complex b) {return complex(a.x+b.x,a.y+b.y);}
complex operator -(complex a,complex b) {return complex(a.x-b.x,a.y-b.y);}
complex operator *(complex a,complex b) {return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}

证明用向量推一推

欧拉公式： e i x = c o s ( x ) + i s i n ( x ) e^{ix}=cos(x)+isin(x) (泰勒级数)
N N 次单位根： 1 1 / n 1^{1/n} ，在复数域中有 n n 个解： e 2 π i k / n e^{2πik/n}
主 N N 次单位根： ω n = e 2 π i / n ω_n=e^{2πi/n}

由于 N N 次单位根的循环性质，若将其作为点值的 x i x_i 将会简化计算至 O ( n l o g n ) O(nlogn)

欧拉公式的证明可以把公式化一化很容易推
主 N N 次单位根可以几何意义来理解，就是复平面上转 n n 次可以回到 x x 轴

complex Wn(cos(2.0*Pi/lim),1.0*type*sin(2.0*Pi/lim));

快速傅里叶变换

（公式不好打直接贴图）
在这里插入图片描述

有点值表达式变回系数表达式是快速傅里叶逆变换，又叫 I F F T IFFT
在这里插入图片描述
图解快速傅里叶变换：
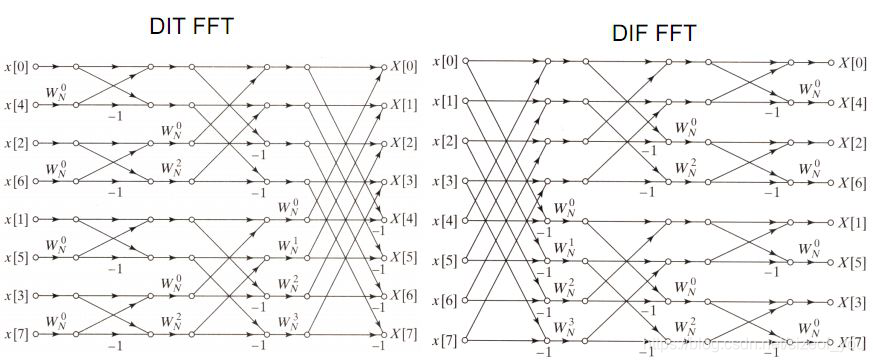
在这里插入图片描述

代码实现的时候 F F T FFT 分递归版和非递归版，递归版就是上面介绍的最基础的，而非递归的要用到蝴蝶变换。

递归版：


void FFT(complex *F,int lim,int type){
    if(lim==1) return;
    complex a1[(lim>>1)+5],a2[(lim>>1)+5];
    for(int i=0;i<=lim;i+=2) a1[i>>1]=F[i],a2[i>>1]=F[i+1];//拆成奇数项和偶数项 
    FFT(a1,lim>>1,type); FFT(a2,lim>>1,type);
    complex Wn(cos(2.0*Pi/lim),1.0*type*sin(2.0*Pi/lim)),w(1,0);
    for(int i=0;i<(lim>>1);i++,w=w*Wn){
        F[i]=a1[i]+w*a2[i];
        F[i+(lim>>1)]=a1[i]-w*a2[i];
    }
}

蝴蝶变换

在这里插入图片描述
在这里插入图片描述
（不知为什么像素如此渣，将就着看qwq）

实现的时候要预处理一个 r e v rev 数组（说实话只要记住就好原理什么的不重要 ）

while(limit<=n+m) limit<<=1,l++;
	for(int i=0;i<limit;i++)
		rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));

非递归版 F F T FFT ：

void fft(complex *F,int type){
	for(int i=0;i<limit;i++)
		if(i<rev[i]) swap(F[i],F[rev[i]]);
	for(int mid=1;mid<limit;mid<<=1){
		complex Wn(cos(Pi/mid),type*sin(Pi/mid));//单位根
		for(int r=mid<<1,j=0;j<limit;j+=r){//r是区间长度，j是位置
			complex w(1,0);//幂
			for(int k=0;k<mid;k++,w=w*Wn){
				complex x=F[j+k],y=w*F[j+mid+k];
				F[j+k]=x+y; F[j+mid+k]=x-y;
			}
		}
	}
}

因为非递归版比递归版常数小所以现在常用非递归版的

例题

luogu3803模板题

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
const int maxn=4e6+10;
const double Pi=acos(-1.0);

inline int rd(){
    int x=0,f=1;char c=' ';
    while(c<'0' || c>'9') f=c=='-'?-1:1,c=getchar();
    while(c<='9' && c>='0') x=x*10+c-'0',c=getchar();
    return x*f;
}

struct complex{
    double x,y;
    complex(double xx=0,double yy=0){x=xx,y=yy;}
}a[maxn],b[maxn];
complex operator +(complex a,complex b) {return complex(a.x+b.x,a.y+b.y);}
complex operator -(complex a,complex b) {return complex(a.x-b.x,a.y-b.y);}
complex operator *(complex a,complex b) {return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}

int n,m,l,rev[maxn],limit=1;

void fft(complex *F,int type){
    for(int i=0;i<limit;i++)
        if(i<rev[i]) swap(F[i],F[rev[i]]);
    for(int mid=1;mid<limit;mid<<=1){
        complex Wn(cos(Pi/mid),type*sin(Pi/mid));//单位根
        for(int r=mid<<1,j=0;j<limit;j+=r){//r是区间长度，j是位置
            complex w(1,0);//幂
            for(int k=0;k<mid;k++,w=w*Wn){
                complex x=F[j+k],y=w*F[j+mid+k];
                F[j+k]=x+y; F[j+mid+k]=x-y;
            }
        }
    }
}

int main(){
    n=rd(); m=rd();
    for(int i=0;i<=n;i++) a[i].x=rd();
    for(int i=0;i<=m;i++) b[i].x=rd();
    while(limit<=n+m) limit<<=1,l++;
    for(int i=0;i<limit;i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
    fft(a,1); fft(b,1);
    for(int i=0;i<=limit;i++) a[i]=a[i]*b[i];
    fft(a,-1);
    for(int i=0;i<=n+m;i++)
        printf("%d ",(int)(a[i].x/limit+0.5));
    return 0;
}

bzoj2179
其实就是 A ∗ B p r o b l e m A*Bproblem 

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#define maxn 240005
using namespace std;
int n,lena,lenb,limit=1,l,rev[maxn],ans[maxn];
char s1[maxn],s2[maxn];
const double Pi=acos(-1.0);
 
struct complex{
    double x,y;
    complex(double xx=0,double yy=0){x=xx,y=yy;}
}a[maxn],b[maxn];
complex operator +(complex a,complex b){return complex(a.x+b.x,a.y+b.y);}
complex operator -(complex a,complex b){return complex(a.x-b.x,a.y-b.y);}
complex operator *(complex a,complex b){return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
 
void FFT(complex *F,int type){
    for(int i=0;i<limit;i++)
        if(i<rev[i]) swap(F[i],F[rev[i]]);
    for(int mid=1;mid<limit;mid<<=1){
        complex Wn(cos(Pi/mid),1.0*type*sin(Pi/mid));
        for(int r=mid<<1,j=0;j<limit;j+=r){
            complex w(1,0);
            for(int k=0;k<mid;k++,w=w*Wn){
                complex x=F[j+k],y=w*F[j+mid+k];
                F[j+k]=x+y,F[j+mid+k]=x-y;
            }
        }
    }
}
 
int main(){
    scanf("%d%s%s",&n,s1,s2); lena=lenb=n-1;
    for(int i=0;i<n;i++) a[n-i-1].x=s1[i]-'0';
    for(int i=0;i<n;i++) b[n-i-1].x=s2[i]-'0';
    while(a[lena].x==0) lena--;
    while(b[lenb].x==0) lenb--;
    while(limit<=lena+lenb) limit<<=1,++l;
    for(int i=0;i<limit;i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
    FFT(a,1);FFT(b,1);
    for(int i=0;i<=limit;i++) a[i]=a[i]*b[i];
    FFT(a,-1);
    for(int i=0;i<=lena+lenb;i++){
        ans[i]+=(int)(a[i].x/limit+0.5);
        if(ans[i]>9) ans[i+1]+=ans[i]/10,ans[i]%=10;
    }
    while(ans[lena+lenb+1]) lena++;
    int now;
    for(now=lena+lenb;now;now--)
        if(ans[now]) break;
    for(;now>=0;now--) printf("%d",ans[now]);
    return 0;
}

bzoj2194
也是非常裸的模板题了，了解性质就能知道把数组翻转一下就好了

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#define maxn 400005
using namespace std;
const double Pi=acos(-1.0);
 
inline int rd(){
    int x=0,f=1;char c=' ';
    while(c<'0' || c>'9') f=c=='-'?-1:1,c=getchar();
    while(c<='9' && c>='0') x=x*10+c-'0',c=getchar();
    return x*f;
}
 
struct complex{
    double x,y;
    complex(double xx=0,double yy=0){x=xx,y=yy;}
}a[maxn],b[maxn];
complex operator +(complex a,complex b){return complex(a.x+b.x,a.y+b.y);}
complex operator -(complex a,complex b){return complex(a.x-b.x,a.y-b.y);}
complex operator *(complex a,complex b){return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
 
int n,limit=1,l,rev[maxn];
 
void FFT(complex *F,int type){
    for(int i=0;i<limit;i++)
        if(i<rev[i]) swap(F[i],F[rev[i]]);
    for(int mid=1;mid<limit;mid<<=1){
        complex Wn(cos(Pi/mid),1.0*type*sin(Pi/mid));
        for(int r=mid<<1,j=0;j<limit;j+=r){
            complex w(1,0);
            for(int k=0;k<mid;k++,w=w*Wn){
                complex x=F[j+k],y=w*F[j+mid+k];
                F[j+k]=x+y,F[j+mid+k]=x-y;
            }
        }
    }
}
 
int main(){
    n=rd();
    for(int i=0;i<n;i++) a[n-i-1].x=rd(),b[i].x=rd();
    while(limit<2*n) limit<<=1,l++;
    for(int i=0;i<limit;i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
    FFT(a,1);FFT(b,1);
    for(int i=0;i<=limit;i++) a[i]=a[i]*b[i];
    FFT(a,-1);
    for(int i=n-1;i>=0;i--) printf("%d\n",(int)(a[i].x/limit+0.5));
    return 0;
}

哦对了多说一句， F F T FFT 通常可以用来解决长这个样子的式子：
c ( n ) = ∑ i = 0 n − 1 a ( i ) × b ( n − i ) c(n)=\sum_{i=0}^{n-1}a(i)\times b(n-i) （这其实就是卷积）
也就是下标和为定值

然后是一些不那么裸的题（但其实还是很裸
ZJOI2014力
把分子和分母分别看成两个多项式然后前面后面分开算，只要翻转一个就好了

#include<iostream>
#include<cstdio>
#include<cmath>
#define maxn 400005
#define LL long long
using namespace std;
const double Pi=acos(-1.0);

struct complex{
    double x,y;
    complex(double xx=0,double yy=0){x=xx,y=yy;}
}a1[maxn],a2[maxn],b[maxn];
complex operator +(complex a,complex b){return complex(a.x+b.x,a.y+b.y);}
complex operator -(complex a,complex b){return complex(a.x-b.x,a.y-b.y);}
complex operator *(complex a,complex b){return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}

int n,rev[maxn],l,limit=1;

inline void FFT(complex *F,int type){
    for(int i=0;i<limit;i++)
        if(i<rev[i]) swap(F[i],F[rev[i]]);
    for(int mid=1;mid<limit;mid<<=1){
        complex Wn(cos(Pi/mid),type*sin(Pi/mid));
        for(int r=mid<<1,j=0;j<limit;j+=r){
            complex w(1,0);
            for(int k=0;k<mid;k++,w=w*Wn){
                complex x=F[j+k],y=w*F[j+k+mid];
                F[j+k]=x+y,F[j+mid+k]=x-y;
            }
        }
    }
}

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%lf",&a1[i].x),a2[n-i+1].x=a1[i].x;
    for(int i=1;i<=n;i++) b[i].x=1.0/i/i;
    while(limit<=2*n) limit<<=1,l++;
    for(int i=0;i<limit;i++) rev[i]=(rev[i>>1]>>1)|((i&1)<<(l-1));
    FFT(a1,1); FFT(b,1);
    for(int i=0;i<=limit;i++) a1[i]=a1[i]*b[i];
    FFT(a1,-1); FFT(a2,1);
    for(int i=0;i<=limit;i++) a2[i]=a2[i]*b[i];
    FFT(a2,-1);
    for(int i=1;i<=n;i++)
        printf("%.5lf\n",(a1[i].x-a2[n-i+1].x)/(double)limit);
    return 0;
}

HNOI2017礼物
bzoj3160fft+manacher
bzoj4503

再说一句这玩意卡精度会死人的。。掉精度掉的很厉害
所以看起来现在出题都用 N T T NTT ？

猜你喜欢

转载自blog.csdn.net/sizeof_you/article/details/84336752
今日推荐
TIOBE 5 月榜单：Fortran “复活”进入 Top 10
GCC 14.1 发布
面壁智能发布 Eurux-8x22B 开源大模型 —— 堪称「理科状元」
开源日报 | 谷歌扶持鸿蒙上位；开源Rabbit R1；Docker加持的安卓手机；微软的焦虑和野心；海尔电器把开放平台关了
中国码农的“35岁魔咒”
蘭雅 CorelDRAW 插件 2024.5.1 国际劳动节版，免费下载
Arc Browser for Windows 1.0 正式 GA
90后程序员开发视频搬运软件、不到一年获利超 700 万，结局很刑！
周排行
Java自定义时间格式
同步整形电路
在开发中最最最常用的字符串的属性大集合
Linux 查看端口占用并杀掉
Java基础四：ArrayList
多线程之死锁就是这么简单
mysql 基础命令集
awk 命令详解
Centos6.3编译安装nginx+php步骤
OCR （Optical Character Recognition，光学字符识别）
每日归档
更多
2024-05-08(42)
2024-05-07(14)
2024-05-06(40)
2024-05-05(0)
2024-05-04(7)
2024-05-03(19)
2024-05-02(0)
2024-05-01(4)
2024-04-30(1)
2024-04-29(40)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022