FFT 快速傅里叶变换学习笔记
基本信息
用途 : 多项式乘法
时间复杂度 : \(O(nlogn)\) (常数略大)
算法过程
基本思路
求 \(H(x) = G(x) \times F(x)\)
直接从系数表达式转化为系数表达式比较难搞, 所以考虑先把 \(F(x),\ G(x)\) 转化为点值表达式, 再 \(O(n)\) 求出 \(H(x)\) 的点值表达式, 然后从 \(H(x)\) 的点值表达式转化为 \(H(x)\) 的系数表达式.
其中, 从系数表达式转化为点集表达式的过程叫 \(DFT\), 又叫 求值运算.
从系数表达式转化为点集表达式的过程叫 \(IDFT\), 又叫 插值运算.
求值运算
先考虑求值运算的过程, 设 \(F(x),G(x)\) 分别为 \(n\) 次, \(m\) 次的多项式, 则 \(H(x)\) 为 \(n+m\) 次的多项式,
所以我们需要求出 \(F(x),G(x)\) 在 \(n+m-1\) 个不同的点处的值, 才能保证最终求得的 \(H(x)\) 的唯一性, (可以类比求函数解析式所需的条件).
如果直接硬算, 复杂度会达到 \(O(n^2)\), 所以我们需要借助一个叫做单位根的神奇东西.
复数
引入单位根之前, 得先介绍一下复数.
首先, 我们定义一个数 \(i\), 使 \(i^2=-1\) (下文中的所有 \(i\) 都表示这个东西).
形如 \(a+bi\) 的数就叫做复数, 其中 \(a,b \in \mathbb{R}\).
复数和实数一样, 也有四则运算 (其实可以类比成多项式的运算).
设 \(x = a+bi, y=c+di\), 则
- $ x+y = (a+c)+(b+d)i $
- $ x-y = (a-c)+(b-d)i $
- $ x \times y = (ac-bd)+(ad+cb)i$ (把 \(x,y\) 当成多项式乘开即可).
- $ \frac{x}{y} = \frac{a+bi}{c+di} = \frac{(a+bi)(c-di)}{(c+di)(c-di)} = \frac{(ac+bd)+(ad+cb)i}{c^2+d^2} $ (类似于无理数运算中分母有理化的过程).
接下来, 我们介绍一个叫 "复平面" 的东西.
长这样

和数轴上的一个点能唯一地表示一个实数类似, 复平面上的一个点能唯一地表示一个复数.
其中, \(x\) 轴上的数为实数 \((real\ axis)\), \(y\) 轴上的数为虚数 \((imaginary\ axis)\).
我们设一个复数的辐角为该复数在复平面上的点对应的向量与 \(x\) 轴逆时针的夹角,
一个复数的模长为该复数对应向量的模长.
我们会得到一个神奇的性质 :
设 \(x,y,z\) 都为复数, 且 \(x \times y = z\), 则 \(z\) 的幅角等于 \(x,y\) 的幅角相加, \(z\) 的模长等于 \(x,y\) 的模长相乘.
如下图 (图源)
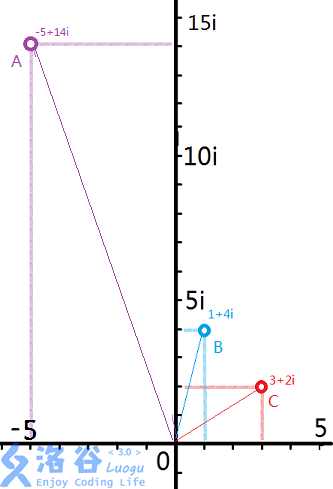
幅角相加可以用三角函数证明, 模长相乘可以把坐标带入直接算就好. (证明过程写出来比较麻烦, 原谅我时间有限)
单位根
有了上面的基础后, 我们就可以来认识单位根了.
定义 : 若复数 \(x^n = 1,\ ( n \in \mathbb{N+})\), 则称 \(x\) 为 \(n\) 次单位根.
考虑一下复数相乘的性质, 可以发现, \(x\) 的模长必然为 \(1\), (大于 \(1\) 的话会越乘越大, 小于 \(1\) 的话会越乘越小),
而 \(x\) 的幅角为 \(\frac{2\pi k}{n},\ (k \in [0,n) )\).
那也就意味着, \(x\) 一定在复平面的单位圆上, 并且将单位圆 \(n\) 等分.
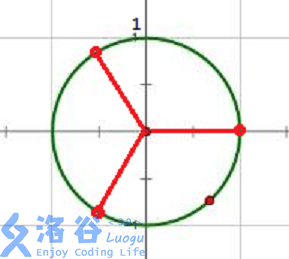
为了便于称呼, 我们用 \(\omega_n\) 来表示 \(n\) 单位根, 并从 \(1\) 开始将他们逐个编上号, \(\omega_n^0 = 1\).
接下来, 我们介绍一些单位根的性质 (原谅我真的没时间....)
- \(\omega_n^k = (\omega_n^1)^k\)
- $\omega_n^0 \omega_n^1 \dots \omega_n^{n-1} $ 互不相等.
- \(\omega_n^{k+\frac{n}{2}} = -\omega_n^k\) (\(n\) 为偶数)
- \(\omega_{2n}^{2k} = \omega_n^k\)
- \(\sum_{k=0}^{n-1} \omega_n^k = 0\) (带入等差数列求和公式即可)
好了, 复数和单位根就介绍到这里, 还记得我们原来要干什么吗?
我们想把 \(F(x)\) 从 系数表达式 转化为 点值表达式 .
求点值表达式, 就需要选择 \(n+m-1\) 个自变量 \(x\) 带入求值.
通常情况下, 这个操作的复杂度是 \(O(n^2)\) 级别的, 但我们的傅里叶大大发现, 把单位根带入求值, 会有神奇的效果.
为了方便描述, 我们这里把 \(n\) 重定义为大于 \(n+m-1\) 的第一个 \(2\) 的正数次方, 并把 \(F(x)\) 重定义为 \(n-1\) 次多项式, 后面多出的系数默认为 \(0\).
把 \(\omega_n^k\) ($ k \in [0,\frac{n}{2})$)带入 \(F(x)\), 得到
\[ F(\omega_n^k) = f[0]\omega_n^0 + f[1]\omega_n^1 + \dots + f[n-1]\omega_n^{n-1} \]
尝试使用分值的思想, 把奇偶次项分开, 得到
\[ F(\omega_n^k) = f[0]\omega_n^0 + f[2]\omega_n^2 + \dots + f[n-2]\omega_n^{n-2} + f[1]\omega_n^1 + f[3]\omega_n^3 + \dots + f[n-1]\omega_n^{n-1} \]
两部分似乎有相似之处,
设
\(G1(x) = f[0]x^0 + f[2]x^1 + f[n-2]x^{\frac{n}{2}-1}\)
\(G2(x) = f[1]x^0 + f[1]x^1 + f[n-1]x^{\frac{n}{2}-1}\)
则
\[ \begin{aligned} F(\omega_n^k) & = G1(\omega_n^{2k}) + \omega_n^kG2(\omega_n^{2k}) \\ & = G1(\omega_{\frac{n}{2}}^{k}) + \omega_n^kG2(\omega_{\frac{n}{2}}^{k}) \end{aligned} \]
若再把 \(\omega_n^{k+\frac{n}{2}}\) 带入 \(F(x)\), 由于 \(\omega_n^{k+\frac{n}{2}} = -\omega_n^k\), 所以他们的偶次项是相同的, 而奇次项是相反的.
也就是
\[ \begin{aligned} F(\omega_n^{k+\frac{n}{2}}) & = G1(\omega_n^{2k + n}) + \omega_n^{k+\frac{n}{2}}G2(\omega_n^{2k + n}) \\ & = G1(\omega_{\frac{n}{2}}^{k}) - \omega_n^kG2(\omega_{\frac{n}{2}}^{k}) \end{aligned} \]
发现 \(F(\omega_n^k)\) 和 \(F(\omega_n^k)\) 化简后得到的式子只有一个符号的差别, 那么意味着, 我们只需算出当 \(k \in [0,\frac{n}{2})\) 时的
\[ G1(\omega_{\frac{n}{2}}^{k}) \]
和
\[ G2(\omega_{\frac{n}{2}}^{k}) \]
这两个式子, 就可以算出 \(\omega_n^0\) 到 \(\omega_n^{n-1}\) 的所有点值.
而上面那两个式子显然 (应该显然吧...) 是可以递归处理的, 那么每次就减少计算一半的点, 时间复杂度就降低到了 \(O(n\log n)\).
放个代码
void trans(cn *f,int len,bool id){
if(len==1) return;
cn *g1=f,*g2=f+len/2; // 直接在 f 数组的地址上修改, 防止使用内存过多
for(int i=0;i<len;i++) tmp[i]=f[i]; // 由于是之间在 f 数组的地址上修改, 所以要备份
for(int i=0;2*i<len;i++){ g1[i]=tmp[i<<1]; g2[i]=tmp[i<<1|1]; }
trans(g1,len/2,id); // 递归处理
trans(g2,len/2,id);
cn w1=(cn){cos(2*Pi/len),sin(2*Pi/len)},wi=(cn){1,0};
if(id) w1.b*=-1;
for(int i=0;2*i<len;i++){
tmp[i]=g1[i]+wi*g2[i]; // 上面的两个式子
tmp[i+len/2]=g1[i]-wi*g2[i];
wi=wi*w1; // 处理出每个单位根
}
for(int i=0;i<len;i++) f[i]=tmp[i];
}那么求值运算, 也就是 \(DFT\) 就大功告成了.
差值运算
我们先用矩阵乘法来表示一下求点值的过程.
设 矩阵\(A\) 为要带入的 \(n\) 个自变量以及它们的 \(0 \sim n\) 次方,
矩阵 \(B\) 为 \(F(x)\) 的系数,
矩阵 \(C\) 为自变量对应的 \(n\) 个点值.
则有
\[ AB = C \]
即

现在我们知道了 \(A\), 知道了 \(C\), 要求 \(B\), 那一般思路就是把 \(A\) 除过去, 即
\[ B = CA^{-1} \]
其中 \(A^{-1}\) 为 \(A\) 的逆矩阵, 它们的乘积为单位矩阵.
经过一系列复杂的运算后, 发现 \(A^{-1}\) 是长这样的, (可以尝试自己手推一下, 需要用到上面单位根的第 4 个性质)
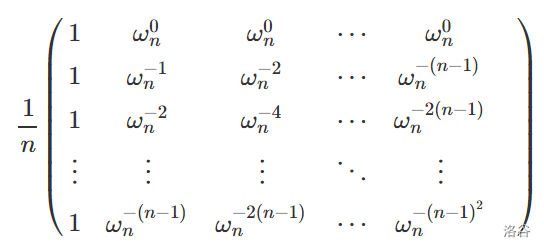
是不是很眼熟,
没错, 实际上就是把 \(A\) 的 \(\omega_n^k\) 全都换成了 \(\omega_n^{-k}\), 并在前面加了个系数.
那 \(CA^{-1}\) 究竟要怎么算呢?
是不是完全没有头绪? (还是只有我一个人是这样)
答案是, 把 \(A^{-1}\) 看做 \(A\), 把 \(C\) 看做 \(B\), 把 \(B\) 看做 \(C\) , 再进行一遍 \(DFT\) 就行了. (说人话).
就是 把点值看做一个新函数的系数, 然后把 \(\omega_n^0 \sim \omega_n^{-(n-1)}\) 带入这个新函数, 求值, 得到的点值再乘上一个 \(\frac{1}{n}\) 就得到了\(H(x)\), 也就是 \(F(x) \times G(x)\) 的系数.
ok, 到此为止, 我们搞定了 \(DFT\) 和 \(IDFT\) ,\(FFT\) 的流程也就到这里了,
放代码.
#include<bits/stdc++.h>
#define _USE_MATH_DEFINES
using namespace std;
const int N=3e6+7;
const double Pi=M_PI;
struct cn{
double a,b;
cn operator + (const cn &x) const{
return (cn){x.a+a,x.b+b};
}
cn operator - (const cn &x) const{
return (cn){a-x.a,b-x.b};
}
cn operator * (const cn &x) const{
return (cn){x.a*a-x.b*b,x.a*b+a*x.b};
}
cn operator *= (const cn &x) const{
return (cn){x.a*a-x.b*b,x.a*b+a*x.b};
}
};
int n,m;
cn f[N],g[N],tmp[N];
void trans(cn *f,int len,bool id){
if(len==1) return;
cn *g1=f,*g2=f+len/2; // 直接在 f 数组的地址上修改, 防止使用内存过多
for(int i=0;i<len;i++) tmp[i]=f[i]; // 由于是之间在 f 数组的地址上修改, 所以要备份
for(int i=0;2*i<len;i++){ g1[i]=tmp[i<<1]; g2[i]=tmp[i<<1|1]; }
trans(g1,len/2,id); // 递归处理
trans(g2,len/2,id);
cn w1=(cn){cos(2*Pi/len),sin(2*Pi/len)},wi=(cn){1,0};
if(id) w1.b*=-1;
for(int i=0;2*i<len;i++){
tmp[i]=g1[i]+wi*g2[i]; // 上面的两个式子
tmp[i+len/2]=g1[i]-wi*g2[i];
wi=wi*w1; // 处理出每个单位根
}
for(int i=0;i<len;i++) f[i]=tmp[i];
}
int main(){
// freopen("FFT.in","r",stdin);
cin>>n>>m;
for(int i=0;i<=n;i++) scanf("%lf",&f[i].a);
for(int i=0;i<=m;i++) scanf("%lf",&g[i].a);
int t=1;
while(t<=n+m) t<<=1;
trans(f,t,0);
trans(g,t,0);
for(int i=0;i<t;i++) f[i]=f[i]*g[i];
trans(f,t,1);
for(int i=0;i<=n+m;i++) printf("%d ",(int)(f[i].a/t+0.49)); //+0.49 减小因精度产生的误差 (我也不知道为什么这样就可减小误差...)
return 0;
}但是, 当你把这份代码交上去后, 会发现只有 77pts, 后面两点会 TLE.
这是因为复数运算的常数本身就比较大, 再加上递归带来的常数, 你不T谁T.
所以, 继续下一个内容.
FFT的优化
复数运算带来的常数是优化不了了, 毕竟 \(FFT\) 的关键步骤 ---- 分治 要依靠它才能进行.
(当然, 有人用其他更优的东西把它替代了, 不过这属于下一个内容 ---- \(NTT\) )
那我们就考虑如何优化递归带来的常数吧.
我们发现, 递归的下传过程并没有进行什么操作, 在上传过程中才处理出了点值.
那我们可以这样理解 : 递归的下传过程就是为了寻找每个数的对应位置.
那么, 这个对应位置是否存在某种规律, 能让我们免去递归的过程, 直接把它们放在应该放的位置?
经过前人的不懈努力和细心观察发现, 每个数最终的位置是该数的 二进制翻转
比如, 当 \(n = 8\) 的时候.
0 1 2 3 4 5 6 7
0 2 4 6 | 1 3 5 7
0 4 | 2 6 | 1 5 | 3 7
0 | 4 | 2 | 6 | 1 | 5 | 3 | 7化为二进制就是
000 001 010 011 100 101 110 111
000 100 010 110 001 101 011 111是不是非常神奇
然后我们可以用一个类似递归的过程来处理他们的位置
for(int i=0;i<n;i++)
num[i]=(num[i>>1]>>1])|((i&1) ?n>>1 :0)可以这样理解,
假设你有一个数 \(x\), 它的二进制为
xxxxxxxxxx把它拆成这两部分
xxxxxxxxx | x前半部分的翻转, 就相当于 \(x>>1\) 的翻转再左移一位. (可以自己模拟一下)
然后再根据最后一位是 \(0\) 或 \(1\) , 在前面补上相应的一位.
ok, 这样, 我们就避免了递归带来的常数.
还有一个小地方
for(int i=0;2*i<len;i++){
tmp[i]=g1[i]+wi*g2[i]; // 上面的两个式子
tmp[i+len/2]=g1[i]-wi*g2[i];
wi=wi*w1; // 处理出每个单位根
}我们可以把它改成
for(int i=0;2*i<len;i++){
cn tmp=wi*g2[i];
tmp[i]=g1[i]+tmp; // 上面的两个式子
tmp[i+len/2]=g1[i]-tmp;
wi=wi*w1; // 处理出每个单位根
}减少了一下复数的运算量.
最终代码 【模板】多项式乘法(FFT)
#include<bits/stdc++.h>
#define _USE_MATH_DEFINES
using namespace std;
const int N=3e6+7;
const double Pi=M_PI;
struct cn{
double a,b;
cn operator + (const cn &x) const{
return (cn){x.a+a,x.b+b};
}
cn operator - (const cn &x) const{
return (cn){a-x.a,b-x.b};
}
cn operator * (const cn &x) const{
return (cn){x.a*a-x.b*b,x.a*b+a*x.b};
}
};
int n,m,t=1,num[N];
cn f[N],g[N],tmp[N];
void trans(cn *f,int id){
for(int i=0;i<t;i++)
if(i<num[i]) swap(f[i],f[num[i]]);
for(int len=2;len<=t;len<<=1){
int gap=len>>1;
cn w1=(cn){cos(2*Pi/len),sin(2*Pi/len)*id};
for(int i=0;i<t;i+=len){
cn wj=(cn){1,0};
for(int j=i;j<i+gap;j++){
cn tt=wj*f[j+gap];
f[j+gap]=f[j]-tt; // 这里需要注意一下赋值的顺序
f[j]=f[j]+tt;
wj=wj*w1;
}
}
}
}
int main(){
//freopen("FFT.in","r",stdin);
//freopen("x.out","w",stdout);
cin>>n>>m;
for(int i=0;i<=n;i++) scanf("%lf",&f[i].a);
for(int i=0;i<=m;i++) scanf("%lf",&g[i].a);
while(t<=n+m) t<<=1; // 保证 t > n+m
for(int i=1;i<t;i++) num[i]=(num[i>>1]>>1)|((i&1)?t>>1:0);
trans(f,1);
trans(g,1);
for(int i=0;i<t;i++) f[i]=f[i]*g[i];
trans(f,-1);
for(int i=0;i<=n+m;i++) printf("%d ",(int)(f[i].a/t+0.49));
return 0;
}
推荐题目
下面三道是 \(NTT\) 的题.
参考资料
傅里叶变换(FFT)学习笔记 by command_block
对了, 还有一件事,
Typora真好用