逻辑回归既是最简单的神经网络, 也是可解释性较强的广义线性回归模型, 同时又是具备概率假设的线性分类模型, 个人认为它是机器学习的一个基础核心. 因此怎么学习都不过分. 复杂的模型虽然有很好的学习能力, 能对非线性数据集进行很好的拟合, 但是往往其背后的原理难以尽知全貌. 而使用逻辑回归模型, 虽然对模型有很好的可解释性,但需要对数据特征有更深刻的认知, 才能构建出更为稳健靠谱的模型. 业界都强调特征工程决定了机器学习算法的上限, (即便是当下火热的深度学习,其各种层也是在进行特征的提取), 而特征工程说白了就是在对数据特征进行筛选, 组合的过程. 因此对数据特征的敏感程度决定了特征工程上限.
这里构造一组二维特征数据, 进行逻辑回归建模, 逐步加入组合特征来验证模型效果.
代码如下:
step1.引入相关库, 并构建一个数据二维特征的数据集.
这里没有将数据集拆分为训练集与测试集, 只是对训练集的验证, 目的不是验证模型的泛化能力, 而是对空间数据点的分割能力. 因为正常人只能对小于3维的空间数据有概念, 因此这里特征只选取了2个维度.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
# create data
x1 = np.array([1, 2, 2, 3, 4, 5, 6, 7, 7]).reshape([-1, 1])
x2 = np.array([4, 3, 5, 1, 4, 1, 3, 6, 1]).reshape([-1, 1])
y = np.array([1, 1, 1, 0, 1, 1, 0, 0, 0]).reshape([-1, 1])
data = np.concatenate((x1, x2, y), axis=1)
step2. 训练一个LR模型, 并输出模型回归系数以及对训练集的预测准确率
x_data = data[:, [0, 1]]
print(x_data)
y_data = y.ravel()
print(x_data.shape, y_data.shape)
# train lr model
lr = LogisticRegression(C=1000, max_iter=1000)
lr.fit(x_data, y_data)
y_pred = lr.predict(x_data)
acc = accuracy_score(y_data, y_pred)
# show coef and accuracy
print(lr.coef_)
print(lr.intercept_)
print("acc = {}".format(acc))output:
[[1 4]
[2 3]
[2 5]
[3 1]
[4 4]
[5 1]
[6 3]
[7 6]
[7 1]]
(9, 2) (9,)
[[-0.95162026 0.27151988]]
[3.57778014]
acc = 0.7777777777777778

输出分别为数据集特征, 数据特征维度, 数据标签维度. LR 模型训练回归系数, 截距, 以及模型的准确率.
step3. 将特征的空间表示出来, 并绘制出模型在空间上的分割.
x = np.array([x for x in np.linspace(0.01, 10, 1000)])
a0 = lr.intercept_[0]
a1 = lr.coef_[0, 0]
a2 = lr.coef_[0, 1]
k = - a1 / a2
b = - a0 / a2
x2 = k * x1 + b
plt.scatter(data[data[:, -1] == 1, 0], data[data[:, -1] == 1, 1], color="red")
plt.scatter(data[data[:, -1] == 0, 0], data[data[:, -1] == 0, 1], color="green")
plt.xlabel("x1")
plt.ylabel("x2")
plt.title("2D features scatter")
# drawn lr model lines on the scatter
plt.plot(x, x2, color="blue")
plt.show() output:
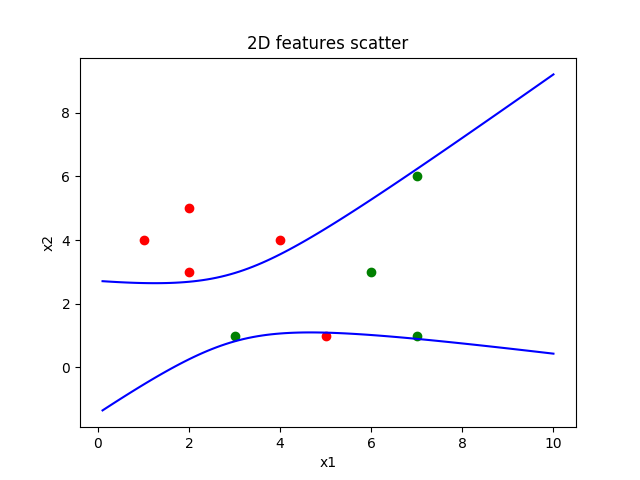
如图所示, 图中的点, 无论如何都不能将其进行线性的分割, 模型最终收敛学习到如上图当中的结果.这是也是单纯线性模型的局限性, 但是模型本身会很简单.
模型最终表达式为: y = 3.57778014 - 0.95162026 * x1 + 0.27151988 * x2
想要让模型能达到非线性效果的分割, 就需要对特征进行组合, 让线性模型转换为多项式的结构为:
y = a1 * x1 + a2 * x2 + a12 * x1 * x2
- 在step1中追加一个特征 x12 = x1 * x2
- 在step2中x_data = data[:, [0, 1, 2]]
- 在step3中增加回归系数的提取a12 = lr.coef_[0, 2],令上述 y = 0,
则方程为 x2 = - (a0 + a1 * x1) / (a2 + a12 * x1)
output:
[[ 1 4 4]
[ 2 3 6]
[ 2 5 10]
[ 3 1 3]
[ 4 4 16]
[ 5 1 5]
[ 6 3 18]
[ 7 6 42]
[ 7 1 7]]
(9, 3) (9,)
[[ 1.567852 8.01291958 -1.6117581 ]]
[-8.47497336]
acc = 0.8888888888888888
如图所示,对数据的空间划分达到了非线性的效果,模型预测的准确率也提升了 10%。
模型最终的表达式为: y = -8.47497336 + 1.567852 * x1 + 8.01291958 * x2 - 1.6117581 * x1 * x2
对这个结果好像还是不太满意,假设给到将特征空间表示的散点图给到一位智力发育正常的小朋友,告诉他画一条线将红点和绿点分开,估计他能很好的完成。因此对该模型再次改进。加入特征的二次项。将模型update为:
y = a1 * x1 + a2 * x2 + a11 * x1**2 + a22 * x2**2 + a12 * x1 * x2
- 在step1中追加三个特征 x11 = x1 * x1, x22 = x2 * x2, x12 = x1 * x2
- 在step2中x_data = data[:, [0, 1, 2, 3, 4]]
- 在step3中增加回归系数的提取 a11 = lr.coef_[0, 2], a22 = lr.coef_[0, 3], a12 = lr.coef_[0, 4],令 y = 0,
则有以下方程:
a = a22
b = a2 + a12 * x
c = a11 * x**2 + a1 * x + a0
ta = b**2 - 4 * a * c
x2_1 = (- b + np.sqrt(ta)) / (2 * a)
x2_2 = (- b - np.sqrt(ta)) / (2 * a)
注:模型包含二次项,二次函数有两个解,故存在两个方程。
output:
[[ 1 4 1 16 4]
[ 2 3 4 9 6]
[ 2 5 4 25 10]
[ 3 1 9 1 3]
[ 4 4 16 16 16]
[ 5 1 25 1 5]
[ 6 3 36 9 18]
[ 7 6 49 36 42]
[ 7 1 49 1 7]]
(9, 5) (9,)
[[14.32769658 -6.82633077 -1.0106934 5.34083449 -4.4611383 ]]
[-20.90001265]
acc = 1.0
如图所示,数据被两条二次曲线很好的分割开来,验证一下准确率也达到了100%。
模型最终的表达式为:y = -20.9 + 14.33 * x1 - 6.83 * x2 -1.01 * x1**2 + 5.34 * x2**2 -4.46 * x1 * x2
综合上所述,通过特征的组合让原本线性模型具备了非线性的效果,其实本质上让线性函数转换为了非线性的函数。因为数据是构造的,现实数据不会这么低维,高维数据本身也不能通过可视化变得可见,虽然可以通过PCA降低维来达到可见的目的,但其会造成信息的损失。而且某些特征本身也可能会是针对某个现实场景建模的噪音。但是其本质还是对特征的选择和组合,达到对空间上数据进行划分的目的。
本文只针对了关于特征组合来提升模型效果,重点在说明特征组合下模型的数学意义,事实上真实数据在训练集上的准确划分并不能一定验证集上准确划分。