1.1 机器人学之空间描述和变换

版权声明：本文为博主原创文章，未经博主允许不得转载。 https://blog.csdn.net/lwz45698752/article/details/84425511

---

参考博文

第一章参考博文

---

• 机器人操作的定义：通过某机构使零件和工具在空间运动——》需要描述这些部件的位姿——》定义和运用表达位姿的数学量——》需要定义坐标系并给出表达规则

描述位置

• 假定存在着一个世界坐标系，世界坐标系是一切坐标系的基础（由世界坐标系定义其他笛卡尔坐标系）
• 空间一点用一矢量描述位置，即用坐标表示
• (A)P:左上标 ，矢量中各元素的数值，是在坐标系A中的各个主轴方向的距离，即沿着每个坐标轴的距离是矢量在相应坐标轴的投影。

描述姿态

• 为了描述姿态，将在物体上固定一个坐标系（称为连体坐标系）并且给出此坐标系相对于参考坐标系的描述。
• A坐标系相对于参考坐标系B的描述，具体来说是，A坐标系的主轴方向的单位矢量在坐标系B中的描述，将这三个矢量按X,Y,Z排成一组，组成3*3的矩阵（一列为一个矢量），称为旋转矩阵，确定姿态
• 以后再讲其他只需要三个参数的姿态描述方法

• 旋转矩阵的行是参考坐标系A在坐标系B中的表达（映射到谁就点乘谁）
• 旋转矩阵是正交阵，而正交阵的逆等于其转置，即旋转矩阵的性质为：两等号，见上图

位姿描述

• 矢量方向：箭头处点相对于箭尾处点的位置
• 位姿用两个坐标系的相对关系来描述（原点的相对关系和姿态的相对关系）
• 位姿——》位置（旋转矩阵为单位阵）
• 位置——》姿态（位置矢量为零矢量）

映射：不同坐标系变换

• 不同坐标系的矢量只有在坐标系的姿态相同时，才能相加
  
• 关注坐标的映射表达（2.13）
• 红笔处的物理意义描述

齐次变换矩阵

• 对式2.17的理解：假想有个中间坐标系，原点同B一样，但姿态和A一样，作姿态变换，然后作平移变换
• 齐次形式便于计算，添加一行，
• 齐次变换矩阵反映了旋转和平移

算子

• 用于坐标系间点的映射的数学表达式为算子，包括点的平移算子，矢量旋转算子，平移加旋转算子。

平移算子

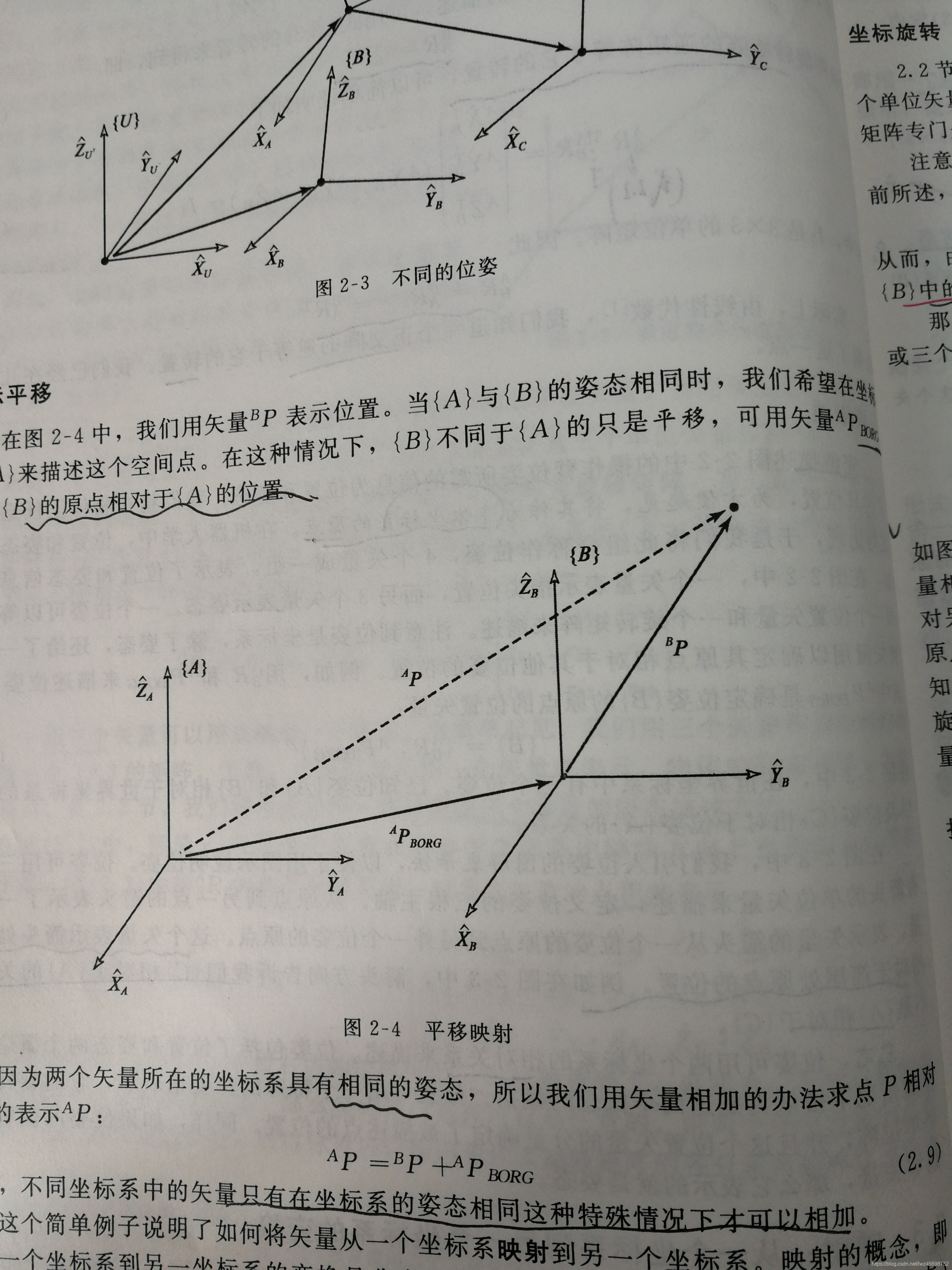
• 关注文中公式即可，即2.24与2.9等价（理解下面所说的表达）
• 空间中点的平移与此点向另一个坐标系的映射具有相同的数学描述
• 矢量向前移动与坐标系向后移动的数学表达式是相同的，观察点不同

旋转算子

• 旋转矩阵R还可以用旋转算子来定义，将一个矢量变换为新的矢量，当旋转矩阵作为算子，无须写出上下标（不涉及两个坐标系），写成
  -

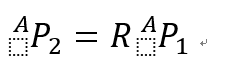• 矢量经过某旋转得到的旋转矩阵与描述某坐标系相对参考坐标系旋转所得到的旋转矩阵是相同的

• R的下标表示绕哪个轴旋转

• 单纯用于矢量的姿态变换，旋转算子算作33，但若考虑到位置和位姿，则44
  
  

• 式2.13与2.27的数学意义相同

• 根据观测点的不同，旋转算子表达为矢量向前旋转或坐标系向后旋转

变换算子

与矢量和旋转矩阵一样，坐标系可通过变换算子来定义。在这个定义中，只涉及一个坐标系，所以符号无上下标。算子T将矢量平移并旋转得到新矢量：

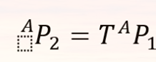
同理，2.13等价于2.18，数学意义相同，解释不同（矢量变换VS坐标系映射）

• 矢量包含旋转与平移的变换与描述某坐标系相对于参考坐标系旋转并平移的变换是相同的
• 变换矩阵T通常是齐次变换形式（广义旋转矩阵+位置矢量分量）

小结

• 坐标系的三主轴的单位矢量来描述姿态
• 符号表示：坐标系B相当于A的旋转矩阵为：上A下B + R 左上标永远为参考坐标系
• 旋转矩阵的各列的模均为1，并且这些单位矢量均相互正交，即其为正交阵
• 旋转矩阵描述姿态变换，定义姿态
• 齐次变换矩阵描述坐标系变换，定义坐标系
• 引入齐次变换矩阵作为一个表达坐标系的一般工具，包含位置和姿态信息的4*4矩阵

---

1. 齐次变换矩阵的三种解释
   1. 位姿的描述（针对坐标系）
   2. 变换映射（点在不同坐标系的表达）
   3. 变换算子（坐标系中的矢量）
2. 位姿与变换数学意义上是相同的，但位姿用于描述，变换用于映射或算子

---

变换的计算

参照开篇博文

注：

• 若有N个未知变换和N个变换方程，则变换可有变换方程求出。
• 采用坐标系的图形表示法，即通过原点间的箭头表示，进一步地，箭头方向表明坐标系定义方式，如相对于A(箭尾)定义坐标系D（箭头）

其他姿态描述方法

• 可参考开篇博文

• 旋转矩阵（标准正交阵）是特殊的各列相互正交的单位阵，其行列式恒为+1

• 考虑用小于9个参数表达姿态，根据凯莱公式，三个参数足够。（本来就三个自由度）

• 旋转矩阵可用三个参数确定，所以9个分量非相互独立，存在6个约束方程

• 进一步地，寻找一种姿态描述法只用三个参数。

• 旋转可看做算子（针对矢量旋转），也可看作对姿态的描述。

X-Y-Z固定角

• 将旋转看为算子依次进行（从右开始），先绕固定坐标系（参考坐标系）的X轴，Y轴，最后Z轴，对应回转角，俯仰角和偏转角（右乘固定坐标系）
• X-Y-Z固定角与旋转矩阵的转换（求解超越方程）

Z-Y-X欧拉角

• 坐标系B与已知参考坐标系A重合，绕Zb,Yb,Xb旋转（绕运动坐标系的各轴旋转）
• 相对运行坐标系的旋转描述是一组欧拉角描述
• 下标上附加撇号代表欧拉角描述的旋转
• 注意一点：左乘运动坐标系，右乘固定坐标系
• Z-Y-X欧拉角与旋转矩阵的转换（求解超越方程，类比固定角）

Z-Y-Z欧拉角

• • 坐标系B与已知参考坐标系A重合，绕Zb,Yb,Zb旋转（绕运动坐标系的Z,Y轴旋转）
• • Z-Y-Z欧拉角与旋转矩阵的转换（见书）

等效角度-轴线表示法

• 右手定则——四指握住旋转轴，拇指指向旋转轴正方向，沿四指指尖方向（弯曲方向）旋转为正方向，反之为负方向。
• 任何姿态可通过选择合适的轴与角度获得
• 将坐标系B与参考坐标系A重合，然后B绕单位矢量K转一定角度（右手定则表正负）
• 矢量K称为有限旋转的等效轴，单位矢量长度恒为1，实际上确定它只需要两个参数，加上旋转角，也即三个参数，正好确定旋转所需要的3个自由度。
• 若该轴为参考坐标系A的主轴时，等效旋转矩阵的表示（见书）
• 一般轴时（过原点的轴），等效旋转矩阵的表示
• 旋转矩阵与轴线表示法的相互转化（旋转矩阵-》轴线表示法：存在多解，且若旋转角为0度，不好确定旋转轴）
• 若旋转轴不过原点，考虑转化（P33例题）

欧拉参数

• 通过四个数值来表示，称为欧拉参数，四个参数的平方和是1，这个关系总是保持不变，因此，姿态可以看做是四维空间中单位超球面上的一点
• 欧拉参数是一个4*1的矢量
• 欧拉参数还可看做是一个3*1的矢量加上一个标量
• 欧拉参数可被视为一个单位四元数
• 欧拉参数与旋转矩阵的相互转化（见书P35）

示教和预定义姿态

• 在机器人系统中，可通过运行机器人来示教位姿，即机械臂运行到某期望位置，记录该位置，此时机器人是六自由度的测量工具，这样进行姿态示教时不需要程序员处理姿态描述问题，另外，示教点是通过旋转矩阵来存储的，但用户看不到。
• 预定义姿态，例如定义向下或向上，但若预定义姿态只对姿态进行描述和定义，则应用范围有限。

自由矢量的变换

• 矢量的类型不同，其变换形式不同
• 矢量的相等和等效有区别，相等即矢量的维数，大小和方向相同，相等矢量可能有不同的作用线（左右平移所得）
• 等效是针对某特定功能来说的，其代表矢量在某功能上产生了相同的作用效果
• 某些特殊情况，不相等的矢量会产生等价的作用效果，即等效的

基本矢量类型

• 线矢量：与作用线相关的矢量，作用效果取决于矢量的大小和方向，如力矢量的作用效果取决于力的作用线（或作用点）
• 自由矢量：可能出现在空间任意位置，若大小和方向不变，则意义也不变，如纯力矩矢量，速度矢量
  • 对于自由矢量，我们只关心大小和方向，所以在两坐标系间间变换只与旋转矩阵有关，原点的相对平移在计算时不涉及，即出现在位置矢量变换中的(上)A-Pborg不能出现在速度变换中

计算成本

• 计算机计算变换时不采用齐次变换形式，避免浪费时间在0,1与其他数字相乘上面，按照式2.41计算（拼接矩阵形式）
• 矩阵乘法两种方法：第一种：从右到左依次相乘，第二种：求出整体变换矩阵，一般而言，第一种运算次数较少
• 当中间变换矩阵都是常量，而你需要将多个矢量在坐标系A中的描述变换为在坐标系B中的描述，推荐第二种，一劳永逸。