前言
上虽然算是学过了但是实质上还是根本什么都不会 看大佬们的模板去A了模题(手动滑稽)
于是下定决心要理解FFT的代码
一些的证明主要是从算法导论和两位大佬的博客上学的 大佬1 大佬2
在这过程中感觉由于一些证明的东西太琐碎和一直没有找到FFT的要点浪费了很多时间
FFT目的
为了快速求出(在longn的时间复杂度)两个系数表达多项式
经过运算后的系数表达多项式
FFT主要思路
因为发现在多项式以点值表达的时候可以
直接用两个多项式下标相同点值的分别进行运算
可以在线性的时间内完成运算
大大降低了时间复杂度
所以考虑如何快速的将一个系数表达的多项式转化为一个点值表达的多项式再转变回来
最暴力的就是直接把各个不同的x代入求出点值
但是这样显然不合理
我们可以利用单位复根的特殊性质来加速这个过程
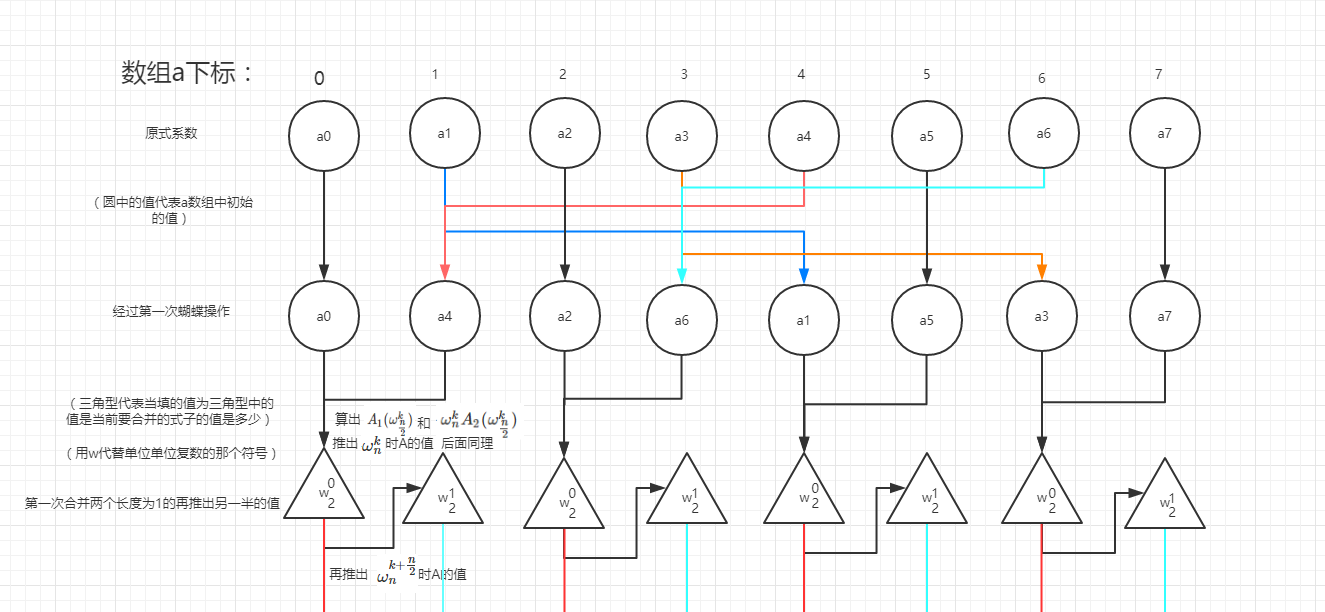
(借用下自为风月马前卒大佬的图)

可以发现两个式子只差中间的一个运算符号
这样在求求出第一个的值的时候可以O(1)求出第二个的值
问题就缩小了一半
这样我们就可以像线段树一样O(nlongn)的时间 递归算出整个式子的各个数带进去的值
点值表达转化回系数表达可以通过单位复根的性质 直接修改单位复根的值就可以了
但是我们发现如果直接递归的话 常数会很大 于是某位大佬找出了迭代(递推)的方法
通过蝴蝶操作O(n)预处理一下 可以快速确定如何分为奇偶两种下标的多项式
递推代码(如果FFT代码中的解释没有看懂可以再看下面的补充)
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define C getchar()-48
inline ll read()
{
ll s=0,r=1;
char c=C;
for(;c<0||c>9;c=C) if(c==-3) r=-1;
for(;c>=0&&c<=9;c=C) s=(s<<3)+(s<<1)+c; return s*r; } #define E complex<double> const int N=;//N记得至少开两倍 const double pi=acos(-1); int n,m,l,r[N]; E a[N],b[N]; void fft(E *a,int f){ for(int i=0;i<n;i++)if(i<r[i])swap(a[i],a[r[i]]);//交换位置 if为了避免重复交换变回原来的 for(int i=1;i<n;i<<=1){//当前合并两个长度为i的值的集合 E wn(cos(pi/i),f*sin(pi/i));//单位复根 将一个圆分成i部分 因为每次要合并i对下标为奇数和欧素的 for(int p=i<<1,j=0;j<n;j+=p){//当前要合并区间的第一个位置p E w(1,0); for(int k=0;k<i;k++,w*=wn){//要合并这个区间的第几个数 E x=a[j+k],y=w*a[j+k+i]; a[j+k]=x+y;a[j+k+i]=x-y; //算出带进去的两个值的结果 } } } } int main(){ n=read();m=read(); for(int i=0;i<=n;i++)a[i]=read(); for(int i=0;i<=m;i++)b[i]=read(); m+=n;for(n=1;n<=m;n<<=1)l++;//乘运算后的长度至少为n+m 运算要求为2的整次幂 for(int i=0;i<n;i++)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));//蝴蝶操作 fft(a,1);fft(b,1);//转化为点值表达 for(int i=0;i<=n;i++)a[i]=a[i]*b[i];//O(n)运算 fft(a,-1);//转化为系数表达 for(int i=0;i<=m;i++)printf("%d ",(int)(a[i].real()/n+0.5)); }
补充
如果想要更好的体验就点链接吧(貌似要先登录):传送门
辛辛苦苦画了一晚上