A 时域数学模型

A.a 预备知识

（1）电容
$i_c(t)=C\frac{du_c(t)}{dt}\qquad u_c(t)=\frac{1}{C}\int i_c(t)dt$
$u_c(0^+)=u_c(0^-)$

（2）电感
$u_L(t)=L\frac{di_L(t)}{dt}\qquad i_L(t)=\frac{1}{L}\int u_L(t)dt$
$i_L(0^+)=i_L(0^-)$

（3）弹簧弹性量
$F=kx=k\int vdt\qquad v=\frac{1}{k}\frac{dF}{dt}\qquad （k称为胡克系数）$

（4）阻尼器（不储存能量，吸收能 $\rightarrow 热能$ ）
阻尼器，是以提供运动的阻力，耗减运动能量的装置。

平动阻尼器
$F=kv=k\frac{dy}{dt}$
K:阻尼系数；F:阻尼力；y:位移。
旋转阻尼器
$T=kw=k\frac{d\theta}{dt}$
$K:阻尼系数；w:旋转角速度；\theta:旋转角度；T:阻尼力矩$

（5）牛顿定律
$F=ma\qquad v=\frac{dx}{dt}\qquad a=\frac{dv}{ct}=\frac{d^2x}{dt^2}$

例子：
在这里插入图片描述

（6）电机
在这里插入图片描述
电枢电压： $u_a(t)$
电枢电流： $i_a(t)$
电磁转矩： $M_m(t)$
电枢回路电压平衡方程(由KVL)：
$u_a(t)=L_a\frac{di_a(t)}{dt}+R_ai_a(t)+E_a$

反电势： $E_a(t)=C_ew_m(t)$ ,与 $u_a(t)$ 反向。
能量损耗：等效成一个纯电阻 $R_a$
电机转矩系数 $C_m$
电磁转矩方程： $M_m(t)=C_mi_a(t)$

电机和负载折合到电动机机轴上的两个变量：

粘性摩擦系数 $f_m$
转动惯量 $J_m$

电动机轴上的转矩平衡方程：
$J_m\frac{dw_m(t)}{dt}+f_mw_m(t)=M_m(t)-M_c(t)$
电动机转速： $w_m(t)$
折合到电动机轴上的总负载转矩 $M_c(t)$

（7）机械齿轮

转速 $w_1,w_2\quad$
齿数 $z_1,z_2$
半径 $r_1,r_2$
粘性摩擦系数 $f_1, f_2$
转动惯量 $J_1,J_2$
原动转矩 $M_m$
负载转矩 $M_1,M_2,M_c$

（8）测速发电机
非电信号转化为电信号。
输入： $w$
输出： $u$
比例系数： $K$
传递特性： $u=Kw$

（9）运算放大器
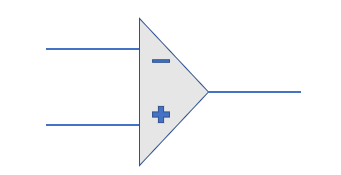
在这里插入图片描述

虚短(运算放大器里面短路)： $u_+=u_-$
虚断（运算放大器里面断开）： $i_+=i_-=0$
实际运放
理想运放
反向接法
同相接法
加法接法
减法接法

A.b 线性系统

重要特性：叠加原理。
线性系统满足：齐次性，也称为均匀性、叠加性。
数学模型：线性定常微分方程 $a_0\frac{d^n}{dt^n}c(t)+a_1\frac{d^{n-1}}{dt^{n-1}}c(t)+...+a_nc(t)=b_0\frac{d^m}{dt^m}r(t)+b_1\frac{d^{m-1}}{dt^{m-1}}r(t)+...+b_mr(t)$

（1）微分方程求解（特征方程法）
$\frac{d^ny}{dt^n}\leftrightarrow s^n$

在这里插入图片描述
二阶齐次通解

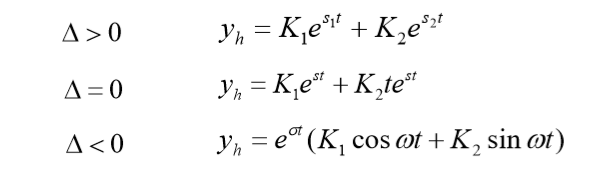
（2）非线性模型的线性化
非线性元件 $\rightarrow$ 线性元件
方法：切线法、小偏差法
切线法，泰勒级数展开：
在这里插入图片描述
小偏差法，二阶泰勒级数展开：

（3）运动的模态（微分方程解中包含哪些要素）
n阶微分方程，n个特征方程根：

无重根： $\lambda_1，\lambda_2，...,\lambda_n$
模态（振型）： $e^{\lambda_1t},e^{\lambda_2t},...,e^{\lambda_nt}$

多重根 : $\lambda$
模态（振型）： $te^{\lambda t},t^2e^{\lambda t}...$

共轭复根： $\lambda=\sigma\pm jw$
共轭复模态（振型） $e^{(\sigma+jw)t}\quad e^{(\sigma-jw)t}$
实函数模态： $e^{\sigma t}sinwt\quad c_2e^{\sigma t}coswt$
齐次通解：
$e^{\sigma t}sinwt+c_2e^{\sigma t}coswt$