自动控制原理(考研)理论篇--第二章(控制系统的数学模型)

导语

本博文基于自动控制原理(胡寿松第六版)全书，将知识点总结，便于同学们的复习，该篇属于自动控制原理的理论篇，理论性东西较多，阅读起来难免有点枯燥，但既然坚持了，那就把它读完吧，因作者也是在复习考研，也是刚毕业的大学生，总结的东西难免会有所纰漏，如发现，请在评论区提醒，望共同进步，考研成功上岸！

2.0 数学模型简单介绍

1. 控制系统的数学模型是描述系统内部物理量(变量)之间关系的数学表达式；
2. 在静态条件下(即变量各阶导数为零)，描述变量之间关系的代数方程叫静态数学模型，描述变量各阶导数之间关系的微分方程叫动态数学模型；
3. 建立控制系统数学模型的方法：分析法、实验法；
   a.分析法：对系统各部分的运动机理进行分析，根据它们依据单位物理规律或化学规律分别列写相应的运动方程，如：牛顿定律、热力学定律、基尔霍夫定律；
   b.实验法：人为地给系统施加某种测试信号，记录其输出响应，并用适当的数学模型去逼近，这种方法称为系统辨识；
4. 时域中常用的数学模型：微分方程、差分方程、状态方程；
5. 复数域中常用的数学模型：传递函数、结构图；
6. 频域中常用的数学模型：频率特性。

2.1 控制系统的时域数学模型

1. 列写元件微分方程的步骤：
   a.根据元件的工作原理及其在控制系统中的作用，确定其输入量和输出量；
   b.分析元件工作中所遵循的物理规律或化学规律，列写相应的微分方程；
   c.消去中间变量，得到输出量与输入量之间关系的微分方程，得到元件时域的数学模型。
   Attention：微分方程标准形式——与输入量有关的项写在方程右端，与输出量有关的项写在方程的左端，方程两端变量的导数项均按降幂排列。
2. 线性系统的基本特性
   线性系统的重要性质：可以应用叠加原理；
   叠加原理的含义：具有可叠加性和齐次性；
   叠加原理：两个外作用同时加于系统所产生的总输出，等于各个外作用单独作用时分别产生的输出之和，且外作用的数值增大若干倍时，其输出亦相应增大同样的倍数。
   实例说明：
   现有线性微分方程如下：
   $$\frac{d^{2}c(t)}{d{t}^2}+\frac{dc(t)}{dt}+c(t)=f(t)$$
   可叠加性：
   $当f(t)=f_1(t)时，上述方程的解为c_1(t)；当f(t)=f_2(t)时，上述方程的解为c_2(t)。如果f(t)=f_1(t)+f_2(t)，方程的解为：c(t)=c_1(t)+c_2(t)$；
   齐次性：
   $当f(t)=A{f}_1(t)时，其中A为常数，则方程的解为：c(t)=A{c}_1(t)$。
3. 线性定常微分方程求解
   求解方法：经典法、拉普拉斯变换法；
   拉普拉斯变换法求解线性定常微分方程的过程：
   a.考虑初始条件，对微分方程中的每一项分别进行拉氏变换，将微分方程转换为变量s的代数方程；
   b.由代数方程求出输出量拉氏变换函数的表达式；
   c.对输出量拉氏变换函数求反变换，得到输出量的时域表达式，即微分方程的解。
4. 非线性微分方程的线性化
   线性化实质：在一个很小的范围内，将非线性特性用一段直线来代替。
   线性化过程：
   设连续变化的非线性函数为$y=f(x)$。
   a.取某平衡状态A为工作点，对应$y_0=f(x_0)，当x=x_0+\Delta x时，有y=y_0+\Delta y$；
   b.$设函数y=f(x)在(x_0,y_0)点连续可微，则将它在该点附近用泰勒级数展开$为
   $$y=f(x)=f(x_0)+(\frac{df(x)}{dx}{)}_{x_0}(x-x_0)+\frac{1}{2!}(\frac{d^{2}f(x)}{d{x}^2}{)}_{x_0}(x-x_0{)}^2+\dots$$
   $当增量x-x_0很小时，略去高次幂项，则有$
   $$y-y_0=f(x)-f(x_0)=(\frac{df(x)}{dx}{)}_{x_0}(x-x_0)$$
   $$\begin{gathered} 令\Delta y=y-y_0=f(x)-f(x_0)，\Delta x=x-x_0，K=(df(x)/dx{)}_{x_0}， \\ 则线性化方程为：\Delta y=K\Delta x，即y=Kx \end{gathered}$$。
5. 运动的模态
   a.
   $如果n阶微分方程的特征根是{\lambda }_1，{\lambda }_2，\dots ，{\lambda }_n且无重根，则把e^{{\lambda }_{1}t}，e^{{\lambda }_{2}t}，\dots ，e^{{\lambda }_{n}t}称为该微分方程所描述运动的模态(振型)。$
   b.
   $每种模态代表一种类型的运动形态，齐次微分方程的通解则是它们的线性组合，即$
   $$y_o(t)=c_1{e}^{{\lambda }_{1}t}+c_2{e}^{{\lambda }_{2}t}+\cdots +c_n{e}^{{\lambda }_{n}t}$$
   $式中，系数c_1,c_2,\dots ,c_n是由初始条件决定的常数。$
   c.
   $如果特征根中有多重根\lambda ,则模态会具有形如t{e}^{\lambda t},t^2{e}^{\lambda t},\dots ,的函数$；
   d.
   $如果特征根中有共轭复根\lambda =\sigma \pm j\omega ,则其共轭复模态e^{(\sigma +j\omega )t}与e^{(\sigma -j\omega )t}可写成实函数模态e^{\sigma t}\sin \omega t与e^{\sigma t}\cos \omega t$。

2.2 控制系统的复数域数学模型

1. 传递函数的定义和性质
   a.定义
   零初始条件下，系统输出量的拉氏变换与输入量的拉氏变换之比。
   设线性定常系统由如下n阶线性常微分方程描述：
   $$\begin{gathered} a_0\frac{d^n}{d{t}^n}c(t)+a_1\frac{d^{n-1}}{d{t}^{n-1}}c(t)+\cdots +a_{n-1}\frac{d}{dt}c(t)+a_{n}c(t) \\ =b_0\frac{d^m}{d{t}^m}r(t)+b_1\frac{d^{m-1}}{d{t}^{m-1}}r(t)+\cdots +b_{m-1}\frac{d}{dt}r(t)+b_{m}r(t) \end{gathered}$$
   $$\begin{gathered} 式中，c(t)是系统输出量；r(t)是系统输入量； \\ {a}_i(i=1,2,\dots ,n)和b_j(j=1,2,\dots ,m)是与系统结构和参数有关的常系数。 \end{gathered}$$
   $注：零初始条件指的是r(t)和c(t)及其各阶导数在t=0时的值均为零。$
   系统的传递函数如下：
   $$G(s)=\frac{C(s)}{R(s)}=\frac{b_0{s}^m+b_1{s}^{m-1}+\cdots +b_{m-1}s+b_m}{a_0{s}^n+a_1{s}^{n-1}+\cdots +a_{n-1}s+a_n}=\frac{M(s)}{N(s)}$$
   $$\begin{gathered} 式中: \\ M(s)=b_0{s}^m+b_1{s}^{m-1}+\cdots +b_{m-1}s+b_m； \\ N(s)=a_0{s}^n+a_1{s}^{n-1}+\cdots +a_{n-1}s+a_n。 \end{gathered}$$
   b.性质
   ① 传递函数是复变量s的有理真分式函数，具有复变函数的所有性质；$m\le n，且所有系数均为实数。$
   ② 传递函数是一种用系统参数表示输出量与输入量之间关系的表达式，它只取决于系统或元件的结构和参数，而与输入量的形式无关，也不反映系统内部的任何信息。
   ③ 传递函数与微分方程有相通性。即传递函数分子多项式及分母多项式系数，分别与相应微分方程的右端及左端微分算符多项式系数相对应。在零初始条件下，将微分方程的算符d/dt用复数s置换得到传递函数；将传递函数多项式中的变量s用算符d/dt置换得到微分方程。
   ④ 传递函数$G(s)$的拉氏反变换是脉冲响应$g(t)$。
   注：$$\begin{gathered} 控制系统的零初始条件的含义： \\ 输入量是在t\ge 0时才作用于系统，在t=0^{-}时，输入量及其各阶导数均为零； \\ 输入量加于系统之前，系统处于稳定的工作状态，即输出量及其各阶导数在t=0^{-}时的值也为零。 \end{gathered}$$
2. 传递函数的零点和极点
   传递函数如下形式时
   $$G(s)=\frac{b_0(s-z_1)(s-z_2)\dots (s-z_m)}{a_0(s-p_1)(s-p_2)\dots (s-p_n)}=K^{\ast }\frac{{\prod }_{i=1}^m(s-z_i)}{{\prod }_{j=1}^n(s-p_j)}$$
   $$\begin{gathered} 式中： \\ {z}_i(i=1,2,\dots ,m)是分子多项式的零点，称为传递函数的零点； \\ {p}_j(j=1,2,\dots ,n)是分母多项式的零点，称为传递函数的极点； \\ 系数K^{\ast }=b_0/a_0称为传递系数或根轨迹增益。 \end{gathered}$$
   传递函数如下面形式时：
   $$G(s)=\frac{b_m({\tau }_{1}s+1)({\tau }_2^2{s}^2+2\zeta {\tau }_{2}s+1)\dots ({\tau }_{i}s+1)}{a_n(T_{1}s+1)(T_2^2{s}^2+2\zeta T_{2}s+1)\dots (T_{j}s+1)}$$
   $$\begin{gathered} 式中： \\ 一次因子对应于实数零极点，二次因子对应于共轭复数零极点； \\ {\tau }_i和T_j称为时间常数；K=b_m/a_n=K^{\ast }{\prod }_{i=1}^m(-z_i)/{\prod }_{j=1}^n(-p_j)称为传递系数或增益。 \end{gathered}$$
3. 传递函数的极点和零点对输出的影响
   a.传递函数的极点决定所描述系统自由运动的模态；
   b.传递函数的零点不形成自由运动的模态，但影响各模态在响应中所占的比重。
4. 典型元部件的传递函数
   a.电位器：电位器是一种把线位移或角位移变换为电压量的装置；一对电位器组成误差检测器。
   单个电位器微分方程：
   $$u(t)=K_1\theta (t)$$
   $$\begin{gathered} 式中：K_1=E/{\theta }_{max}，是电刷单位角位移对应的输出电压，称为电位器传递系数， \\ E是电位器电源电压，{\theta }_{max}是电位器最大工作角。 \end{gathered}$$
   一对相同的电位器组成误差检测器微分方程为：
   $$u(t)=u_1(t)-u_2(t)=K_1[{\theta }_1(t)-{\theta }_2(t)]=K_1\Delta \theta (t)$$
   $$\begin{gathered} 式中： \\ {K}_1是单个电位器的传递系数； \\ \Delta \theta (t)={\theta }_1(t)-{\theta }_2(t)是两个电位器电刷角位移之差，称为误差角。 \end{gathered}$$
   b.测速发电机：测速发电机用于测量角速度并将它转换为电压量的装置。
   永磁式直流测速发电机微分方程为：
   $$u(t)=K_t\omega (t)=K_t\frac{d\theta (t)}{dt}$$
   $$\begin{gathered} 式中： \\ \theta (t)是转子角位移； \\ \omega (t)=\frac{d\theta (t)}{dt}是转子角速度； \\ {K}_t是测速发电机输出斜率，表示单位角速度的输出电压。 \end{gathered}$$
   c.电枢控制直流伺服电动机：电枢控制的直流伺服电动机在控制系统中广泛用作执行机构，用来对被控对象的机械运动实现快速控制。
   电枢控制直流电动机微分方程为：
   $$T_m\frac{d{\omega }_m(t)}{dt}+{\omega }_m(t)=K_m{u}_a(t)-K_c{M}_c(t)$$
   $$\begin{gathered} 式中： \\ {T}_m=R_a{J}_m/(R_a{f}_m+C_m{C}_e)是电动机机电时间常数； \\ {K}_m=C_m/(R_a{f}_m+C_m{C}_e)，K_c=R_a/(R_a{f}_m+C_m{C}_e)是电动机传递系数； \\ {R}_a是电枢电路电阻，J_m是电动机和负载折合到电动机轴上的转动惯量； \\ {f}_m是电动机和负载折合到电动机轴上的黏性摩擦系数； \\ {u}_a是电枢电压，{\omega }_m(t)是电动机转速，M_c(t)是折合到电动机轴上的总负载转矩； \\ {C}_m是电动机转矩系数，C_e是反电势系数。 \end{gathered}$$
   d.无源网络：为了改善控制系统的性能，常在系统中引入无源网络作为校正元件，通常由电阻、电容、电感组成。
   求取无源网络传递函数的方法：
   ① 先列写网络的微分方程，在零初始条件下进行拉氏变换；
   ② 引用复数阻抗直接列写网络的代数方程，求传递函数；用复数阻抗表示电阻时仍为$R$，电容$C$的复数阻抗为$1/Cs$，电感$L$的复数阻抗为$Ls$。

2.3 控制系统的结构图与信号流图

1. 系统结构图的组成和绘制
   信号线：信号线是带箭头的直线，箭头表示信号的流向，在直线旁标记信号的时间函数或象函数；
   引出点(测量点)：引出点表示信号引出或测量的位置，从同一位置引出的信号在数值和性质方面完全相同；
   比较点(或综合点)：比较点表示对两个以上的信号进行加减运算，"+“表示相加，”-"表示相减；
   方框：方框表示对信号进行的数学变换，方框中写入元部件或系统的传递函数，方框的输出变量等于方框的输入变量与传递函数的乘积。
   结构图绘制流程：
   a.考虑负载效应分别列写各元部件的微分方程或传递函数，并用方框表示；
   b.根据各元部件的信号流向，用信号线依次将各方框连接得到系统的结构图。
2. 结构图的等效变换和简化
   本知识点已经在控制系统$Matlab$建模篇详细叙述，小伙伴们可以到相应博文去学习，链接: 结构图等效变换和简化.
3. 信号流图的组成和性质
   典型的信号流图如下：
   
   信号流图的基本性质：
   a.节点标志系统的变量；
   b.支路相当于乘法器，信号流经支路时，被乘以支路增益而变换为另一信号；
   c.信号在支路上只能沿箭头单向传递；
   d.对于给定的系统，节点变量的设置是任意的，因此信号流图不是唯一的。
   信号流图的常用术语：
   a.源节点(输入节点)：源节点上，只有信号输出的支路，没有信号输入的支路，一般代表系统的输入变量；
   b.阱节点(输出节点)：阱节点上，只有输入支路，没有输出支路，一般代表系统的输出变量；
   c.混合节点：既有输入支路又有输出支路；
   d.前向通路：信号从输入节点到输出节点传递时，每个节点只通过一次的通路；前向通路上各支路增益之乘积，称为前向通路总增益，一般用$p_k$表示；
   e.回路：起点和终点在同一节点，而且信号通过每一节点不多于一次的闭合通路称为单独回路；回路中所有支路增益之乘积叫回路增益，用$L_a$表示；
   f.不接触回路：回路之间没有公共节点时，称为不接触回路。
4. 信号流图的绘制
   a.由系统微分方程绘制信号流图。
   方法：含有微分或积分的线性方程，一般通过拉氏变换，将微分方程或积分方程变换为$s$的代数方程后再画信号流图；
   b.由系统结构图绘制信号流图。
   方法：在结构图的信号线上用小圆圈标志出传递的信号，得到节点；用标有传递函数的线段代替结构图中的方框，得到支路，即可得到信号流图。
   注意：
   a.支路增益为1的相邻两个节点，一般可以合并为一个节点，但对于源节点和阱节点不能合并掉；
   b.在结构图比较点之前没有引出点(在比较点之后可以有引出点)时，只需在比较点后设置一个节点即可；
   c.在结构图比较点之前有引出点时，需要在引出点和比较点各设置一个节点。(如果错误合并比较点和引出点，可能造成回路的错误，增加或减少回路的个数)
5. 梅森增益公式
   a.梅森增益公式的来源：按克莱姆规则求解线性联立方程式组时，将解的分子多项式及分母多项式与信号流图巧妙联系的结果。
   b.梅森增益公式表述
   具有任意条前向通路及任意个单独回路和不接触回路的复杂信号流图，求取从任意源节点到任意阱节点之间传递函数。
   $$P=\frac{1}{\Delta }\sum _{k=1}^n{p}_k{\Delta }_k$$
   $$\begin{gathered} 式中： \\ P为从源节点到阱节点的传递函数(总增益)； \\ n为从源节点到阱节点的前向通路总数； \\ {p}_k为从源节点到阱节点的第k条前向通路总增益； \\ \Delta 为1-\sum L_a+\sum L_b{L}_c-\sum L_d{L}_e{L}_f+\dots 称为流图特征式； \\ \sum L_a为所有单独回路增益之和； \\ \sum L_b{L}_c为所有互不接触的单独回路中，每次取其中两个回路的回路增益的乘积之和； \\ \sum L_d{L}_e{L}_f为所有互不接触的单独回路中，每次取其中三个回路的回路增益的乘积之和； \\ {\Delta }_k为流图余因子式，它等于流图特征式中除去与第k条前向通路相接触的回路增益项(包括回路增益的乘积项)以后的余项式 \end{gathered}$$。
6. 闭环系统的传递函数
   反馈控制系统的典型结构图和信号流图如下：
   
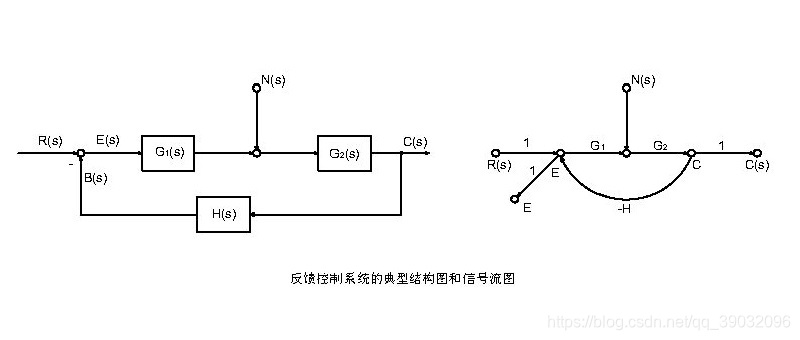
   a. 输入信号作用下的闭环传递函数
   令$N(s)=0$，直接求得输入信号$R(s)$到输出信号$C(s)$之间的传递函数为：
   $$\Phi (s)=\frac{C(s)}{R(s)}=\frac{G_1(s)G_2(s)}{1+G_1(s)G_2(s)H(s)}$$
   $$C(s)=\Phi (s)R(s)=\frac{G_1(s)G_2(s)}{1+G_1(s)G_2(s)H(s)}R(s)$$
   上式表明：系统在输入信号作用下的输出响应$C(s)$，取决于闭环传递函数$C(s)/R(s)$及输入信号$R(s)$的形式。
   b.扰动作用下的闭环传递函数
   令$R(s)=0$，直接求得扰动作用$N(s)$到输出信号$C(s)$之间的传递函数为：
   $${\Phi }_n(s)=\frac{C(s)}{N(s)}=\frac{G_2(s)}{1+G_1(s)G_2(s)H(s)}$$
   $$C(s)={\Phi }_n(s)N(s)=\frac{G_2(s)}{1+G_1(s)G_2(s)H(s)}N(s)$$
   c.输入信号$R(s)$和扰动作用$N(s)$同时作用时系统的输出为：
   $$C(s)=\Phi (s)R(s)+{\Phi }_n(s)N(s)=\frac{G_1(s)G_2(s)R(s)+G_2(s)N(s)}{1+G_1(s)G_2(s)H(s)}$$
   d.闭环系统的误差传递函数
   闭环系统在输入信号和扰动作用时，以误差信号$E(s)$作为输出量时的传递函数称为误差传递函数。
   由典型反馈控制系统得到如下传递函数：
   $${\Phi }_e(s)=\frac{C(s)}{R(s)}=\frac{1}{1+G_1(s)G_2(s)H(s)}$$
   $${\Phi }_{en}(s)=\frac{E(s)}{N(s)}=\frac{-G_2(s)H(s)}{1+G_1(s)G_2(s)H(s)}$$
   $$\begin{gathered} 式中： \\ {G}_1(s)G_2(s)H(s)是回路增益，并称为上述典型控制系统的开环传递函数，等效为主反馈断开时，从输入信号R(s)到反馈信号B(s)之间的传递函数 \end{gathered}$$。

2.4 控制系统建模实例

实例分析：电力牵引电机控制
实例背景叙述：大部分现代列车和调度机车都采用电力牵引电机，牵引电机牵引轨道车辆系统的原理框图如下图(a)，其中电枢控制电机采用大功率直流电机，其参数如下表所示，功率放大器采用差分放大器。


问题：要求建立控制系统的数学模型，计算系统的传递函数$\Omega (s)/{\Omega }_d(s)$，并适当选择差分放大器的电阻$R_1，R_2，R_3，R_4$。
解：
选择转速计来产生一个与输出速度成比例的电压$v_t$，并将它作为差分放大器的一个输入，如图(b)所示。

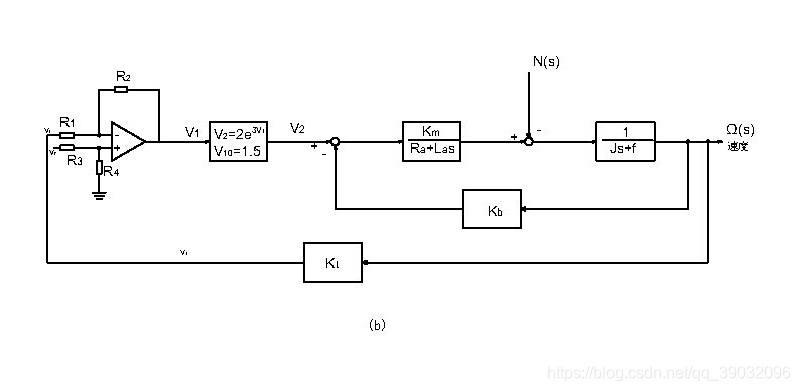
功率放大器是非线性的，可近似表示为指数函数
$$v_2=2e^{3v_1}=g(v_1)$$
其正常工作点为$v_{10}=1.5V$。利用小偏差线性化的方法，得到：
$$\Delta v_2=\frac{dg(v_1)}{d{v}_1}{|}_{v_{10}}\cdot \Delta v_1=540\Delta v_1$$
以小增量作为新的变量，省去“$\Delta$”符号，经拉氏变换得到：
$$V_2(s)=540V_1(s)$$
对于差分放大器，则有：
$$v_1=\frac{1+\frac{R_2}{R_1}}{1+\frac{R_3}{R_4}}{v}_r-\frac{R_2}{R_1}{v}_t$$
通常，希望输入控制电压$v_r$在数值上与预期速度${\omega }_d(t)$相等，注意到车辆在稳定运行时由$v_t=K_t{\omega }_d$，于是车辆稳定运行时有：
$$v_1=\frac{1+\frac{R_2}{R_1}}{1+\frac{R_3}{R_4}}{v}_r-\frac{R_2}{R_1}{K}_t{v}_r$$
$其中，v_1=0。当K_t=0.1时，选择\frac{1+R_2/R_1}{1+R_3/R_4}=\frac{R_2}{R_1}{K}_t=1，求出$
$$\frac{R_2}{R_1}=10，\frac{R_3}{R_4}=10$$
系统结构图如（c）所示：

信号流图如下图(d)所示：

由信号流图和梅森增益公式，得到系统闭环传递函数：
$$\frac{\Omega (s)}{{\Omega }_d(s)}=\frac{540G_1(s)G_2(s)}{1+0.1G_1(s)G_2(s)+540G_1(s)G_2(s)}$$
$$\begin{gathered} 代入： \\ {G}_1(s)=\frac{10}{s+1}；G_2(s)=\frac{1}{2s+0.5} \end{gathered}$$
结果为：
$$\frac{\Omega (s)}{{\Omega }_d(s)}=\frac{2700}{s^2+1.25s+2700.75}$$