自动控制原理笔记（2）——控制系统的数学模型

前言

汇总版在这篇文章：自动控制原理上课笔记

控制系统的数学模型

数学模型

• 静态模型：代数方程在静态条件下（即变量各阶导数为零），描述变量之间关系的代数方程。
• 动态模型：微分方程、差分方程、状态方程等。

---

控制系统属于动态系统

• 描述连续系统运动输入输出关系的为微分方程。
• 描述离散系统运动输入输出关系的为差分方程。
• 描述输入、输出和内部各变量间关系的为状态方程。

范围	描述
时域	微分方程（差分方程）
复数域	传递函数（脉冲传递函数）
频域	频率特性

微分方程

列写元件微分方程的步骤可归纳如下：

1. 根据元件的工作原理及其在控制系统中的作用，确定其输入量和输出量。
2. 分析元件工作中所遵循的物理规律或化学规律，列写相应的微分方程。
3. 消去中间变量，得到输出量与输入量之间关系的微分方程，便是元件时域的数学模型。一般情况下，应将微分方程写为标准形式，即与输入量有关的项写在方程的右端，与输出量有关的项写在方程的左端，方程两端变量的导数项均按降幂排列。

---

• 建立控制系统的微分方程时

  一般先由系统原理线路图画出系统方块图，并分别列写组成系统各元件的微分方程；然后，消去中间变量便得到描述系统输出量与输入量之间关系的微分方程。

• 列写系统各元件的微分方程时

  • 应注意信号传送的单向性，即前一个元件的输出是后一个元件的输入，一级一级地单向传送。
  • 应注意前后连接的两个元件中，后级对前级的负载效应。

---

微分方程的解 = 齐次微分方程的通解 + 非齐次微分方程的任一特解。

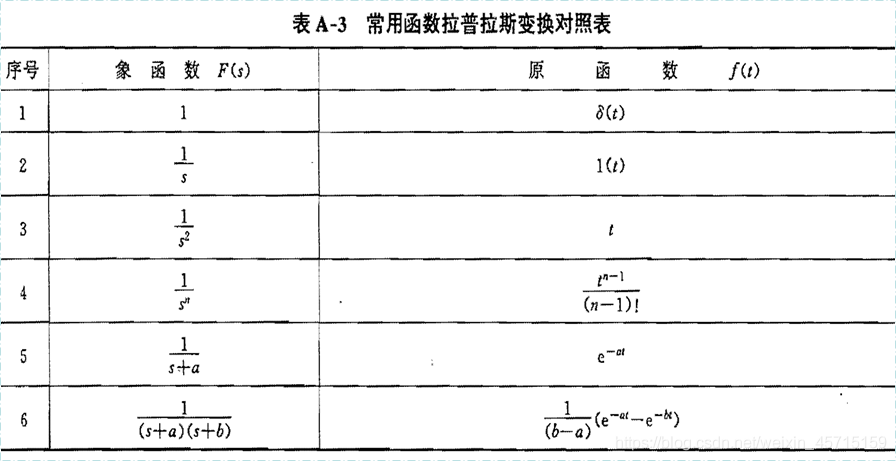
用拉氏变换法求解线性定常微分方程的过程可归结如下：

• 考虑初始条件，对微分方程中的每一项分别进行拉氏变换,将变量 t (时域)的微分方程转换为变量 s (复域)的代数方程。
• 由代数方程求出输出量拉氏变换函数的表达式。
• 对输出量拉氏变换函数求拉氏反变换，得到输出量时域表达式，即为所求微分方程的解。

小偏差法

将非线性微分方程线性化——小偏差法

• 实际工作点在某一平衡点 (x0, y0) 附近

• 非线性 $y=f(x)$ 连续可导

• $x$ 在一个很小的范围内变化，$\Delta x$ 很小（小偏差）

• 可列写线性化增量方程：

  $\Delta y=K\Delta x$ $K=\frac{df(x)}{dx}{|}_{x=x_0}$

传递函数

线性定常系统传递函数的定义：零初始条件下，系统输出量的拉氏变换与输入量的拉氏变换之比。

• 传递函数是复变量 s 的有理真分式函数，具有复变函数的所有性质。

• 传递函数是一种用系统参数表示输出量与输入量之间关系的表达式它只取决于系统或元件的结构和参数，而与输入量的形式无关，也不反映系统内部的任何信息。

• 传递函数与微分方程具有相通性

  • 传递函数分子多项式系数及分母多项式系数，分别与相应微分方程的右端及左端微分算符多项式系数相对应。
  • 将微分方程的算符 $\frac{d}{dt}$ 用复数 s 置换便得到传递函数；反之，将传递函数多项式中的变量s用算符 $\frac{d}{dt}$ 置换便得到微分方程。

---

传递函数是在零初始条件下定义的。控制系统的零初始条件有两方面的含义：

• 指输入量是在 t ≥ 0 时才作用于系统，因此，输入量及其各阶导数在 t = 0 时均为零。

• 指输入量加于系统之前，系统处于稳定的工作状态，即输出量及其各阶导数在 t = 0 时的值也为零，现实的工程控制系统多属此类情况。因此，传递函数可表征控制系统的动态性能，并用以求出在给定输入量时系统的零初始条件响应，即由拉氏变换的卷积定理，有：
  $$c(t)=L^{-1}[C(s)]=L^{-1}[G(s)R(s)]={\int }_0^{t}r(\tau )g(t-\tau )d\tau ={\int }_0^{t}r(t-\tau )g(\tau )d\tau$$

  式中，$g(t)=L^{-1}[G(s)]$ 是系统的脉冲响应。

• 传递函数 $G(s)$ 的拉氏反变换是脉冲响应 $g(t)$

• 脉冲响应（也称脉冲过渡函数）$g(t)$ 是系统在单位脉冲 $\delta (t)$ 输入时的输出响应

---

传递函数的表达形式

• 一般表达形式
  $$G(s)=\frac{C(s)}{R(s)}=\frac{b_0{s}^m+b_1{s}^{m-1}+...+b_{m-1}s+b_m}{a_0{s}^n+a_1{s}^{n-1}+...+a_{n-1}s+a_n}=\frac{M(s)}{N(s)}$$

• 零-极点表达形式——最高阶次项系数为1
  $$G(s)=\frac{b_0(s-z_1)(s-z_2)...(s-z_m)}{a_0(s-p_1)(s-p_2)...(s-p_n)}=K^{\ast }\frac{{\prod }_{i=1}^m(s-z_i)}{{\prod }_{j=1}^n(s-p_j)}$$
  系数 $K^{\ast }=b_0/a_0$ 称为传递系数或根轨迹增益。这种用零点和极点表示传递函数的方法在根轨迹法中使用较多。

  在复数平面上表示传递函数的零点和极点的图形，称为传递函数的零极点分布图。在图中一般用 “o” 表示零点，用 “×” 表示极点。传递函数零极点分布图可以更形象地反映系统的全面特性。

• 典型环节形式——常数项系数为1
  $$G(s)=\frac{b_m({\tau }_{1}s+1)({\tau }_{2}s+1)...({\tau }_{m}s+1)}{a_n(T_{1}s+1)(T_{2}s+1)...(T_{n}s+1)}=K\frac{{\prod }_{i=1}^m({\tau }_{i}s+1)}{{\prod }_{j=1}^n(T_{j}s+1)}$$
  $K$ 称传递系数或增益。传递函数这种表示形式在频率法中使用较多。

---

传递函数的极点就是微分方程的特征根，极点/特征根决定了所描述系统自由运动(零输入响应)的模态。

传递函数的零点并不形成自由运动的模态，但它们却影响各模态响应中所占的比重(系数)，因而也影响响应曲线的形状。

系统产生的运动（响应）分为：

• 强迫运动（零初始条件响应）。

• 自由运动（零输入响应），是系统“固有”的成分。

典型环节

• 比例环节

• 积分环节

• 惯性环节（非周期环节）

• 振荡环节
  $$G(s)=\frac{C(s)}{R(s)}=\frac{{w_n}^2}{s^2+2\zeta w_{n}s+{w_n}^2}=\frac{1}{T^2{s}^2+2\zeta Ts+1}$$

• 微分环节

  • 理想微分环节（与积分环节对应）
  • 一阶微分环节（与惯性环节对应）
  • 二阶微分环节（与振荡环节对应）

• 延迟环节

  • 时域表示 $c(t)=r(t-\tau )l(t-\tau )$
  • 复域表示 $G(s)=\frac{C(s)}{R(s)}=e^{-\tau s}$

控制系统的结构图

控制系统的结构图是由许多对信号进行单向运算的方框和一些信号流向线组成。

它包含四种基本单元：

• 信号线: 信号线是带有箭头的直线，箭头表示信号流向，在直线旁标记信号的时间函数或象函数。
• 引出点(或测量点): 引出点表示信号引出或测量的位置，从同一位置引出的信号在数值和性质上完全相同。
• 比较点(或综合点): 比较点表示对两个以上的信号进行加减运算，+号表示相加，-号表示相减，+号可省不写
• 方框(或环节): 方框表示对信号进行的数学变换,方框中写入元部件/系统传递函数;方框的输出变量等于方框的输入变量与传递函数的乘积,即 C(s) = G(s)U(s)。因此，方框可视作单向运算的算子

系统结构图也是控制系统的一种数学模型。

建议：第1个方程最好能包含输入,相加点,输出。

---

信号流图与结构图的关系

• 节点表示系统的变量。
• 支路相当于乘法器。

信号流图的相关概念

• 前向通路：信号从输入节点到输出节点传递时，每个节点只通过一次的通路，叫前向通路。
• 前向通路总增益：前向通路上各支路增益之乘积，称前向通路总增益，一般用 $p_k$ 表示。
• 回路：起点和终点在同一节点，而且信号通过每一节点不多于一次的闭合通路称为单独回路，简称回路。
• 回路增益：回路中所有支路增益之乘积叫回路增益,用 $L_a$ 表示。
• 不接触回路：回路与回路之间没有公共节点时，这种回路叫做不接触回路。可以有两个或两个以上不接触的回路。
• 不接触回路增益：$L_b{L}_c$ 为所有互不接触的单独回路中,每次取其中2个回路的回路增益的乘积；$L_d{L}_e{L}_f$为所有互不接触的单独回路中,每次取其中3个回路的回路增益的乘积。

梅森增益公式

求取从任意源节点到任意阱节点之间传递函数的梅森增益公式记为：
$$P=\frac{1}{\Delta }\sum _{k=1}^n{p}_k{\Delta }_k$$

• $P$ 为从源节点到阱节点的传递函数(或总增益)。
• $n$ 为从源节点到阱节点的前向通路总数。
• $p_k$ 为从源节点到阱节点的第k条前向通路总增益。
• $\Delta$ 为流图特征式, $\Delta =1-\sum L_a+\sum L_b{L}_c-\sum L_d{L}_e{L}_f+\dots$
  • $\sum L_a$ 为所有单独回路增益之和。
  • $\sum L_b{L}_c$ 为所有互不接触的单独回路中，每次取其中两个回路的回路增益的乘积之和。
  • $\sum L_d{L}_e{L}_f$ 为所有互不接触的单独回路中，每次取其中三个回路的回路增益的乘积之和。
• ${\Delta }_k$ 为流图特征式的余因子式，它等于流图特征式 $\Delta$ 中除去与第 k 条前向通路相接触的回路增益项（包括回路增益的乘积项）以后的余项式。

---

• 为了研究有用输入作用对系统输出 $C(s)$ 的影响，需要求有用输入作用下的闭环传递函数 $C(s)/R(s)$。
• 为了研究扰动作用 $N(s)$ 对系统输出 $C(s)$ 的影响，也需要求取扰动作用下的闭环传递函数 $C(s)/N(s)$。
• 此外，在控制系统的分析和设计中，还常用到在输入信号 $R(s)$ 或扰动 $N(s)$ 作用下，以误差信号 $E(s)$ 作为输出量的闭环误差传递函数 $E(s)/R(s)$ 或 $E(s)/N(s)$。

在一定条件下，系统的输出只取决于反馈通路传递函数 $H(s)$ 及输入信号 $R(s)$，既与前向通路传递函数无关，也不受扰动作用的影响。特别是当 $H(s)=1$，即单位反馈时，$C(s)\approx R(s)$，从而近似实现了对输入信号的完全复现，且对扰动具有较强的抑制能力。

绝不允许将各种闭环传递函数进行叠加后求其输出响应。