分而治之算法

分而治之算法是一个我们生活中经常会用到的算法，当一个问题比较大时我们会将其分割为相同的几个小问题进行解决，因为小问题相同所以一个小问题的算法又能直接应用于其他小问题，所以分而治之经常用到的方法是递归。
下面将通过几个例子来介绍分而治之算法：
1.矩阵计算问题
矩阵A*B=C计算的一般方法是A的第i行元素乘以B的第j列元素得到C的第i行j列的元素。这样的方式虽然很简单，但是却要花费巨额的计算量得不偿失，所以可以使用分治的方法来简化计算。
我们首先将一个矩阵平均的分为四块，然后将这四块元素当成2*2的矩阵进行计算，而在计算块矩阵之间的乘法时我们再次进行分块，直到分块矩阵达到我们规定的不可分大小时直接进行计算。这样得到结果后，我们在将得到的结果按照原有样式进行组合即可得到结果。
经过计算分块的方式虽然能够很好的降低计算量，但是分块和组合却要浪费额外的计算量，所以这个方法其实还要更慢。
不过有人在分块的基础上提出了Strassen算法，这就使得分块的速度要大于直接计算的速度了：
Strassen算法：
$D=A_1(B_2-B_4)$
$E=A_4(B_3-B_1)$
$F=(A_3+A_4)B_1$
$G=(A_1+A_2)B_4$
$H=(A_3-A_1)(B_1+B_2)$
$I=(A_2-A_4)(B_3+B_4)$
$J=(A_1+A_4)(B_1+B_4)$
然后有：
$C1=E+I+J-G$
$C2=D+G$
$C3=E+F$
$C4=D+H+J-F$
通过上述算法我们发现当矩阵的大小大于8时Strassen算法的速度要大于普通算法，所以我们一般将最小不可分割矩阵的大小设置为8（小于等于8用原始方法求解）。
（上述问题书上没提供程序）

2.金块问题：计算8块金块中最重和最轻的金块。
分治步骤：
1.我们设定最小不可分的大小为2。
2.首先将8块分为两个4块,然后4个二块。
3.然后对每个二块进行比较找出最大最小值，然后对找出的四个最大或者最小再次进行比较（是先比较12，和34然后胜者在进行比较）即可得到最大与最小值。
但是当比较元素太多我们一般不采取递归的方法，下面是该算法的非递归代码（思路有点差异，但是差不多）：

//在a[0:n-1]中找出最小值和最大值的非递归程序
template<class T>
bool minmax(T a[],int n,int &indexOfMin,int& indexOfMax)
{//在a[0:n-1]中确定最轻和最重元素的位置，如果少于一个元素，返回false
if(n<1) return false;
if(n==1)
{
    indexOfMin=indexOfMax=0;
    return true;
}
//n>1
int s=1;//奇数情况下的循环起点
if(n%2==1)//n为奇数,则将最初的最大值和最小值都设为0位置的元素，然后在对剩余的偶数元素进行二分法查找
indexOfMin=indexOfMax=0;
else
{//当n是偶数的时候首先比较的一对元素
if(a[0]>a[1])
    indexOfMax=0;indexOfMin=1;
else
    indexOfMax=1;indexOfMin=0;
s=2;
}

//比较剩余元素对
for(int i=s;i<n;i+=2)
{//比较a[i]和a[i+1]，然后将较重者和a[indexOfMax]比较，较轻者和a[indexOfMin]比较
if(a[i]>a[i+1])
{
    if(a[i]>a[indexOfMax])
        indexOfMax=i;
    if(a[i+1]<a[indexOfMin])
        indexOfMin=i+1;
}
else
{
    if(a[i+1]>a[indexOfMax])
        indexOfMax=i+1;
    if(a[i]<a[indexOfMin])
        indexOfMin=i;
}
}
    return true;    
}

上述代码并没有一层层的往上进行比较，而是另最开始的一个或者两个为最大和最小，然后用后面的比较结果与其进行比较，然后大的被更新为indexOfMax, 小的被更新为indexOfMin，当比较完成，最大的就是indexOfMax,最小的就是indexOfMin.

3.残缺棋盘
残缺棋盘书上讲的是真的难理解，这里我贴一个博客地址：
https://blog.csdn.net/gzj_1101/article/details/49368143
为了方便我将其转载到这里（侵删）：

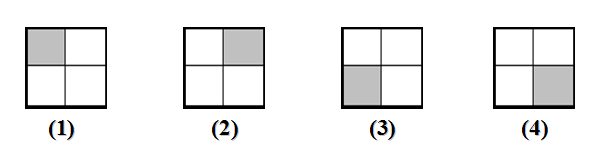
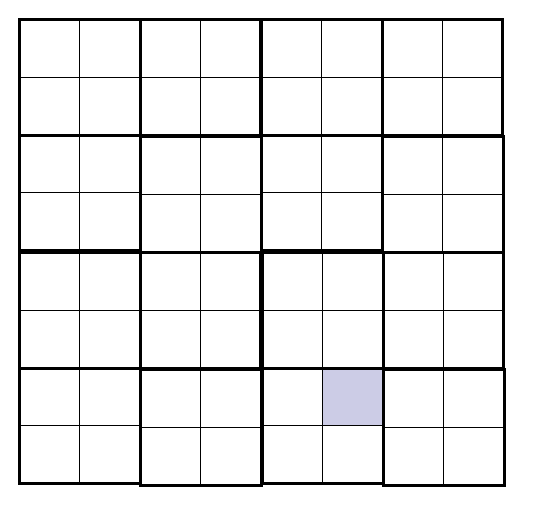
 残缺棋盘是一个2^k*2^个方格的棋盘，其中恰有1个方格残缺。图中给出，其中残缺部分用阴影表示。

这样的棋盘称为”三格板”，残缺棋盘问题就是用这四种三格板覆盖更大的残缺棋盘。再次覆盖中要求:

(1)两个三格板不能重复。

(2)三格板不能覆盖残缺棋盘方格，但必须覆盖到其他所有的方格。

算法思路:

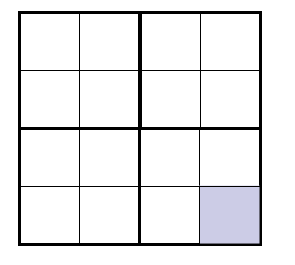
利用分治算法将棋盘细化，逐步解决,以4*4为例

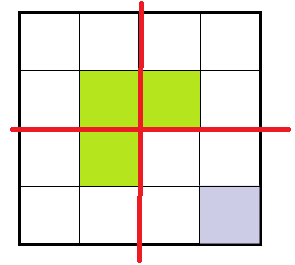
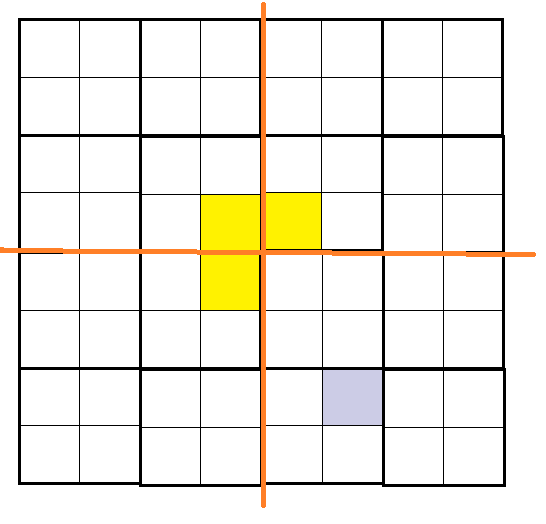
首先判断残缺的位置在哪里，然后在中间填上对应的三格板，如在上图中间拼上三角板(4)，变成下面这样

然后通过中间将其分成了4个2*2的小残缺棋盘，从而问题得以解决

4*4的分析过于简单，现在我们以8*8为例进行分析，能更清楚的理解这个例子中分治算法的思想

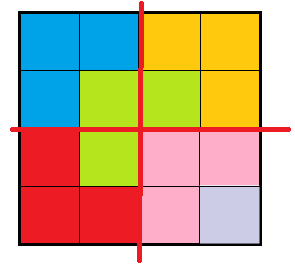
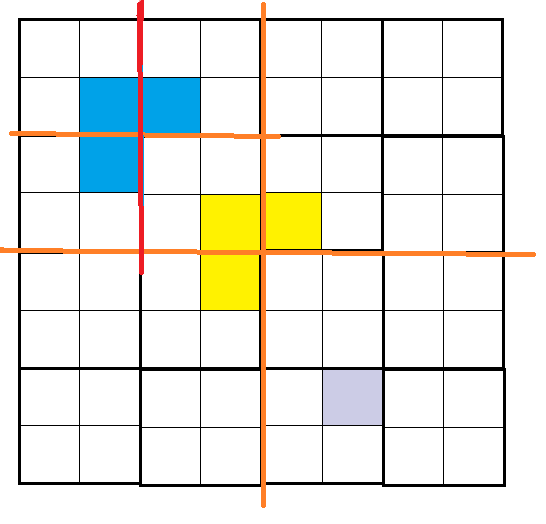
首先将三格板放置在中间，将其分4个小的4*4的残缺棋盘

通过红色线将其划分成4个4*4的残缺棋盘，现在以左上的残缺棋盘为例

然后将左的4*4的小棋盘右划分成了4个2*2的小棋盘，这样就将问题优化成了2*2的三角棋盘的小问题，这样很快就能将左上的4*4的残缺棋盘解决了

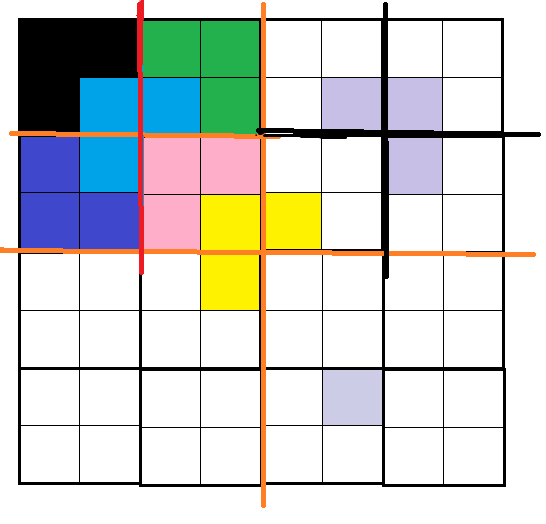
下面继续分析右上的4*4的棋盘，根据残缺的方格在小棋盘中的位置，在中间选择合适的三格板将小的残缺棋盘继续划分，将问题分化成更小的状态

接着的问题和上面一样分析。右上角的小棋盘很快也能解决了，下面两块残缺棋盘的分析方法和上面的一样，整个问题就这样一步步的分解成小问题，然后解决了。

下面是源代码

    
    
#include <iostream>

using namespace std;

int amount,Board[ 100][ 100];

void Cover(int tr,int tc,int dr,int dc,int size)
{
int s,t;
if(size< 2)
return ;
amount++;
t=amount;
s=size/ 2;
if(dr<tr+s&&dc<tc+s) //残缺在左上角
{
//覆盖中间位置
Board[tr+s -1][tc+s]=t;
Board[tr+s][tc+s -1]=t;
Board[tr+s][tc+s]=t;

Cover(tr,tc,dr,dc,s); //覆盖左上
Cover(tr,tc+s,tr+s -1,tc+s,s); //覆盖右上
Cover(tr+s,tc,tr+s,tc+s -1,s); //覆盖左下
Cover(tr+s,tc+s,tr+s,tc+s,s); //覆盖右下
}
else if(dr<tr+s&&dc>=tc+s) //残缺在右上角
{
Board[tr+s -1][tc+s -1]=t;
Board[tr+s][tc+s -1]=t;
Board[tr+s][tc+s]=t;

Cover(tr,tc,tr+s -1,tc+s -1,s);
Cover(tr,tc+s,dr,dc,s);
Cover(tr+s,tc,tr+s,tc+s -1,s);
Cover(tr+s,tc+s,tr+s,tc+s,s);
}
else if(dr>=tr+s&&dc<tc+s) //残缺在左下
{
Board[tr+s -1][tc+s -1]=t;
Board[tr+s -1][tc+s]=t;
Board[tr+s][tc+s]=t;

Cover(tr,tc,tr+s -1,tc+s -1,s);
Cover(tr,tc+s,tr+s -1,tc+s,s);
Cover(tr+s,tc,dr,dc,s);
Cover(tr+s,tc+s,tr+s,tc+s,s);
}
else
{
Board[tr+s -1][tc+s -1]=t;
Board[tr+s -1][tc+s]=t;
Board[tr+s][tc+s -1]=t;

Cover(tr,tc,tr+s -1,tc+s -1,s);
Cover(tr,tc+s,tr+s -1,tc+s,s);
Cover(tr+s,tc,tr+s,tc+s -1,s);
Cover(tr+s,tc+s,dr,dc,s);
}
}

void Print(int s)
{
for( int i= 1;i<=s;i++)
{
for( int j= 1;j<=s;j++)
printf( “%5d “,Board[i][j]);
printf( “\n”);
}
}

int main()
{
int s= 1,k,x,y;
printf( “输入2残缺棋盘的规模:2^k,k=”);
scanf( “%d”,&k);
for( int i= 1;i<=k;i++)
s*= 2;
printf( “输入棋盘残缺位置(x,y):”);
scanf( “%d%d”,&x,&y);
Board[x][y]= 0;
Cover( 1, 1,x,y,s);
Print(s);
return 0;
}
    
    

            </div>

4.归并排序
归并排序是一个利用分治算法的排序算法，其平均速度能达到nlogn是一个非常不错的排序算法。归并排序的主要步骤是分割和归并。
伪码：

void sort(E,n)
{//对E中的n个元素排序，k是全局变量
if(n>=k)
{
    i=n/k;//将n个元素平均分为k块，i为每块的大小
    j=n-i;
    令A由前E的前i个元素组成
    令B由E剩余的j个元素组成
    sort(A,i);//对i个元素进行递归
    sort(B,j);//对剩余的元素进行递归
    merge(A,B,E,i,j);//把A和B合并到E，
}
    else
        对E插入排序//当要排序的元素个数小于k使，使用插入排序进行排序。
}

对最小单元之所以用插入排序是因为当元素很少时，插入排序的速度要更快。
当k=2时，我们称之为2路归并排序，上述伪码的细化版如下：

void mergeSort(T *a,int left,int right)
{//对数组元素a[left:right]排序
if(left<right)
{//至少两个元素
    int middle=(left+right)/2;
    mergeSort(a,left,middle);
    mergeSoer(a,middle+1,right);
    merge(a,b,left,middle,right);//从a到b归并
    copy(b,a,left,right);//将排序结果复制到a。
}   
}

以上代码首先将数组a进行分割，直到最后剩下两个元素，然后将这两个元素归并到b，然后再复制到a，对每组都进行这样的操作（merge代码并未给出）。

以上代码由于每次都做了归并到b然后复制回a的操作，必将浪费很多时间，所以还能够进行改进。

template<class T>
void mergeSort(T a[],int n)
{//使用归并排序对a[0:n-1]排序
T *b=new T[n];
int segmentSize=1;
while(segmentSize<n)
{
    mergePass(a,b,n,segmentSize);
    segmentSize+=segmentSize;
    mergePass(b,a,n,segmentSize);
    segmentSize+=segmentSize;
}
delete[] b;

}

template<class T>
void mergePass(T x[],T y[], int n,int segmentSize)
{//从x到y归并相邻的数据段
int i=0;
while(i<=n-2*segmentSize)//对n-2*segmentSize的数据进行归并处理
{//从x到y归并相邻的数据段
merge(x,y,i,i+segmentSize-1,i+2*segmentSize-1);//对相邻的数据进行归并处理
i=i+2*segmentSize;//更新下一个归并数据段的其实位置

}
//少于两个满数据段
if(i+segmentSize<n)
    //剩余两个数据段
merge(x,y,i,i+segmentSize-1,n-1);
else
    //只剩一个数据段，复制到y
for(int j=i;j<n;j++)
    y[j]=x[j];

}

template<class T>
void merge(T c[],T d[],int startOfFirst,int endOfFirst,int endOfSecond)
{//把相邻两个数据段从c归并到d
int first=startOfFirst;//第一个数据段的索引
int second=endOfFirst+1;//第二个数据段的索引
int result=startOfFirst;//归并数据段的索引

//知道有一个数据段归并到d
while((first<=endOfFirst)&&(second<=endOfSecond))
    if(c[first]<c[second])
        d[result++]=c[first++];
    else
        d[result++]=c[second++];
    //归并剩余元素
    if(first>endOfFirst)
        for(q=second;q<endOfSecond;q++)
            d[result++]=c[q];
        else
            for(q=first;q<endOfFirst;q++)
            d[result++]=c[q];   
}

上述代码并不是一个递归，首先segmentSize=1,即每个段为1，然后将其归并到b，这时b的[1,2],[3,4]等相邻元素时排好序的，然后令segmentSize=2,再从b归并到a，这时a里面的每四个元素时排好序的，然后令segmentsize=4,再次从a归并到b，一直到segmentsize=n,这时所有的数据都排序完成。
注意：这里要注意剩余数据段的处理，当mergePass中只剩余一个数据段的时候，直接复制到y，这时是没有排序的，但是当segmentsize变大时，总有一个会变成剩余两个数据段（少于两个满数据段）的情况，这时会启动merge对剩余数据段进行排序。

上述的排序称为直接归并排序，还有一种归并排序称为自然归并排序，自然归并排序主要是认定分割点的方法与直接归并排序不同，自然归并排序的分割点认定发放是：
从左到右扫描序列元素，若位置i的元素比位置i+1的元素大，则位置i便是一个分割点。自然分割法的最坏情况是逆序，最好情况是正序。

5.快速排序
快速排序的原理其实很简单，首先选取数组中的一个值（一般选取最左边的一个值）将其当做中间值，然后将比这个值小的元素放在该元素的左边，大的放在该元素的右边。然后对左边和右边的元素采取同样的做法，最后我们的元素得到排序。

template<class T>
void quickSort(T a[],int n)
{//对a[0:n-1]快速排序
if(n<=1) return;
//把最大的元素移到数组右端
int max=indexOfMax(a,n);
swap(a[n-1],a[max]);
quickSort(a,0,n-2);
}

之所以先要将最大值移到最右边，是因为我们之后不会判断最右边一个值与中间值的大小。

template<class T>
void quickSort(T a[],int leftEnd,int rightEnd)
{//对a[leftEnd:rightEnd] a[rightEnd+1]>=a[leftEnd:rightEnd]
if[leftEnd>rightEnd] return;

int leftCursor=leftEnd,  //从左到右移动的索引
rightCursor=rightEnd+1;  //从右到左移动的索引（注意：这里加了一个1）
T pivot=a[leftEnd];      //这里直接选取最左边的数字作为中间值
//将位于左侧不小于支点的元素和位于右侧不大于支点的元素交换。
while(true)
{
    do
    {//寻找左侧不小于支点的元素
    leftCursor++;   
    }while(a[leftCursor]<pivot);

    do
    {//寻找右侧不大于支点的元素
    rightCursor--;
    }while(a[rightCursor]>pivot);

    if(leftCursor>=rightCursor) break;//没有找到交换的元素对
    swap(a[leftCursor],a[rightCursor]);
}
//放置支点
a[leftEnd]=a[rightCursor];//将rightCursor和leftEnd交换，这样pivot中值到了他本该的位置。
a[rightCursor]=pivot;

quickSort(a,leftEnd,rightCursor-1);//对左侧的数据段进行排序
quickSort(a,rightCursor+1,rightEnd);//对右侧的数段排序
}

上述代码其实就是一个两边夹逼的原理。

当我们选取的中间值为最大或者最小时，上述代码的速度最慢，这时我们可以采取三值取中规则选择支点元素来避免出现上述的情况。
三值取中快速排序：在三元素a[leftEnd], a[(leftEnd+rightEnd)/2]和a[rightEnd]中选择大小居中的中值元素作为支点元素。我们只需要将上述选择的元素和a[left]交换就可以直接使用上述的代码了。

性能测量（对于较大n）：
快速排序>归并排序>堆排序>插入排序。
性能测量（对于较小n）
插入排序最好（所以我们可以对快速排序的最小分割使用插入排序）。
以上以平均速度为准。

6.选择
问题描述：从n元素数组a[0:n-1]中找出k小的元素。
求解策略：首先对n个元素进行排序，然后取出a[k-1]中的元素。这里我们使用快排对元素进行排序。
我们首先找到中值点，然后进行一个排序得到中值点的顺序，然后将k与中值点进行比较，如果比中值点小，则对前面的元素采用快速排序，再次获取前面数据的中间值的顺序，再次比较，再次排序，直到中间点的位置即为我们要找的元素。

template<class T>
T select(T a[],int leftEnd,int rightEnd,int k)
{
//返回a[leftEnd:rightEnd]中第k小的元素
if(leftEnd>=rightEnd)
    return a[leftEnd];
int leftCursor=leftEnd, rightCursor=rightCursor+1;
T pivot=a[leftEnd];

//将左面不小于支点的元素和右面不大于支点的元素交换
while(true)
{
    do
    {
        leftCursor++;
    }while(a[leftCursor]<pivot);
    do
    {
        rightCursor--;
    }while(a[rightCursor]>pivot);

    if(leftCursor>=rightCursor) break; //交换的一对元素没有找到
    swap(a[leftCursor],a[rightCursor]);     
}
if(rightCursor-leftEnd+1==k)//找到了直接返回
    return pivot;
//放置支点元素
a[leftEnd]=a[rightCursor];
a[rightCursor]=pivot;
//对一个数据段调用递归
if(rightCursor-leftEnd+1<k)
    return select(a,rightCursor+1,rightEnd,k-rightCursor+leftEnd-1);//最后一个参数更新了k的值
else
    return select(a,leftEnd,rightCursor-1,k);
}

7.相距最近的点对
首先上伪码：

if(n不大)
{
    用直接方法求出相距最近的点。
    return;
}
//n很大
把点集分为大致相等的两部分A和B。
分别确定A和B中相距最近的点对。
确定一点在A另一点在B的相距最近的点对。
在上面得到的相距最近的三个点对中，选择相距最近的一对。

求解距离最近的点分三类求解，首先将点集分为两个部分，A和B，然后分别求取A和B中的最近的点并比较出最近的一个，然后求出一个在A中和一个在B中的最近的点对，并与最小值进行对比。
在我们求出A中和B中的最小点对后我们称之大小为$\delta$,然后在求第三类点的时候首先去除离分割线大于等于$\delta$的点，然后任意选取一个在A中$\delta$范围内的点，并选取B中$\delta$范围内并y值与A中选择点的距离小于$\delta$的点。求出距离然后比较。

pointPair closestPair(point1 x[],int numberOfPoints)
{//返回x[0:numberOfPoints-1]中相距最近的点
//如果点的个数少于2，则抛出异常
int n=numberOfPoints;
if(n<2)
    throw illegalParameterValue("Number of points must be > 1");
//按x坐标排序
mergeSort(x,n);
//创建一个类型为point2的数组y，按y坐标排序
point2 *y=new point2 [n];
for(int i=0;i<n;i++)
    //把点i从x复制到y，且记录i在数组x中的索引
    y[i]=point2(x[i].x,x[i].y,i);
mergeSort(y,n);   //按y坐标排序
//创建一个临时数组
point2 *z=new point2 [n];
//寻找相距最近的点对
return closestPair(x,y,z,0,n-1);
}

以上数组创建了三个数组x,y,z其中x数组中的点按照坐标x进行排序，y数组中的点按照点的y坐标进行排序，z为一个空数组。
这里point1,point2,pointPair都是从point中继承而来，不同的是point1中增加了一个整形的数据成员id，point2中增加了一个整形数据类型p，指向点在数组x中的位置。pointPair中有两个点都是point1类型，且增加了一个double型的dist距离。

pointPair closestPair(point1 x[],point2 y[],point2 z[],int l,int r)
{//按x坐标对x[1:r]排序，r>1
//按y坐标对y[1:r]进行排序
//z[1:r]用作临时空间
//返回在x[1:r]中相距最近的点对
if(r-l==1)//仅有两个点
    return pointPair(x[l],x[r],dist(x[l],x[r]));
if(r-l==2)
{//有三个点计算所有点对之间的距离
double d1=dist(x[l],x[l+1]);
double d2=dist(x[l+1],x[r]);
double d1=dist(x[l],x[r]);
//寻找距离相近的两个点
if(d1<=d2&&d1<=d3)
    return pointPair(x[l],x[l+1],d1);
if(d2<d3)
    return pointPair(x[l+1],x[r],d2);
else
    return pointPair(x[l],x[r],d3); 
}   
//多余三个点，划分为两组
int m=(l+r)/2;                 //将x[1:m]归于A,其余归于B
//将有序数组y分前后两部分复制到z[1:m]和z[m+1:r]
int f=l;
int g=m+1;
for(int i=l;i<=r;i++)        //注意了这里p是y[i]在数组x中的索引
    if(y[i].p>m) z[g++]=y[i];
    else z[f++]=y[i];

//分别在两部分中求解相距最近的点
pointPair best=closestPair(x,z,y,l,m);
pointPair right=closestPair(x,z,y,m+1,r);

//确定相距更近的点对
if(right.dist<best.dist)
    best=right;
merge(z,y,l,m,r);  //把z归并到y,重建数组y

//把距中线更近的点放入数组z
int k=1;          //数组z的下标
for(int i=1;i<=r;i++)
    if(fabs(x[m].x-y[i].x)<best.dist)//x[m]是位于中线的点
        z[k++]=y[i];
//检查z[1:k-1]的所有点对，寻找更相近的第三类点对
for(int i=1;i<k;i++)
{
    for(int j=i+1;j<k&&z[j].y-z[i].y<best.dist;j++)//这里检查了位于第三类区中的所有点对，就算是位于同一边的也检查了。
    {
        double dp=dist(z[i],z[j]);
        if(dp<best.dist)
            best=pointPair(x[z[i].p],x[z[j].p],dp);
    }
}
    return best;
}

以上代码有很多细节值得注意，首先将y中的数据复制到z中的时候是根据点y[i]在数组x中的id与m进行比较决定的。由于是按照点在数组x的id与m进行比较，所以x中id大于m的点始终会在z中m位置的后面，其他的在m位置前面，而由于y数组的点是按照y坐标进行排序的，所以后面添加进z数组的点的y坐标一定比前面添加进的点的y坐标要大。这样就使得z数组中的数据为x数组从m处截断前面的点按照y坐标进行排序，后面的点也按照y坐标进行排序。
将z归并到y的程序书上没给这个有点令人难受。
然后最后在比较第三类点的时候，是将所有满足条件的点全部进行了比较，而不仅仅是左边的点和右边的点进行比较。
这里为了避免重复比较也使用了一点技巧。
这个程序有个缺点就是每次都是从x的中间分割，而没有从y中间分割过，这样会使得数据量不平衡。

 残缺棋盘是一个2^k*2^个方格的棋盘，其中恰有1个方格残缺。图中给出，其中残缺部分用阴影表示。

这样的棋盘称为”三格板”，残缺棋盘问题就是用这四种三格板覆盖更大的残缺棋盘。再次覆盖中要求:

(1)两个三格板不能重复。

(2)三格板不能覆盖残缺棋盘方格，但必须覆盖到其他所有的方格。

算法思路:

利用分治算法将棋盘细化，逐步解决,以4*4为例

首先判断残缺的位置在哪里，然后在中间填上对应的三格板，如在上图中间拼上三角板(4)，变成下面这样

然后通过中间将其分成了4个2*2的小残缺棋盘，从而问题得以解决

4*4的分析过于简单，现在我们以8*8为例进行分析，能更清楚的理解这个例子中分治算法的思想

首先将三格板放置在中间，将其分4个小的4*4的残缺棋盘

通过红色线将其划分成4个4*4的残缺棋盘，现在以左上的残缺棋盘为例

然后将左的4*4的小棋盘右划分成了4个2*2的小棋盘，这样就将问题优化成了2*2的三角棋盘的小问题，这样很快就能将左上的4*4的残缺棋盘解决了

下面继续分析右上的4*4的棋盘，根据残缺的方格在小棋盘中的位置，在中间选择合适的三格板将小的残缺棋盘继续划分，将问题分化成更小的状态

接着的问题和上面一样分析。右上角的小棋盘很快也能解决了，下面两块残缺棋盘的分析方法和上面的一样，整个问题就这样一步步的分解成小问题，然后解决了。

下面是源代码

  
  
#include <iostream>

using namespace std;

int amount,Board[ 100][ 100];

void Cover(int tr,int tc,int dr,int dc,int size)
{
int s,t;
if(size< 2)
return ;
amount++;
t=amount;
s=size/ 2;
if(dr<tr+s&&dc<tc+s) //残缺在左上角
{
//覆盖中间位置
Board[tr+s -1][tc+s]=t;
Board[tr+s][tc+s -1]=t;
Board[tr+s][tc+s]=t;

Cover(tr,tc,dr,dc,s); //覆盖左上
Cover(tr,tc+s,tr+s -1,tc+s,s); //覆盖右上
Cover(tr+s,tc,tr+s,tc+s -1,s); //覆盖左下
Cover(tr+s,tc+s,tr+s,tc+s,s); //覆盖右下
}
else if(dr<tr+s&&dc>=tc+s) //残缺在右上角
{
Board[tr+s -1][tc+s -1]=t;
Board[tr+s][tc+s -1]=t;
Board[tr+s][tc+s]=t;

Cover(tr,tc,tr+s -1,tc+s -1,s);
Cover(tr,tc+s,dr,dc,s);
Cover(tr+s,tc,tr+s,tc+s -1,s);
Cover(tr+s,tc+s,tr+s,tc+s,s);
}
else if(dr>=tr+s&&dc<tc+s) //残缺在左下
{
Board[tr+s -1][tc+s -1]=t;
Board[tr+s -1][tc+s]=t;
Board[tr+s][tc+s]=t;

Cover(tr,tc,tr+s -1,tc+s -1,s);
Cover(tr,tc+s,tr+s -1,tc+s,s);
Cover(tr+s,tc,dr,dc,s);
Cover(tr+s,tc+s,tr+s,tc+s,s);
}
else
{
Board[tr+s -1][tc+s -1]=t;
Board[tr+s -1][tc+s]=t;
Board[tr+s][tc+s -1]=t;

Cover(tr,tc,tr+s -1,tc+s -1,s);
Cover(tr,tc+s,tr+s -1,tc+s,s);
Cover(tr+s,tc,tr+s,tc+s -1,s);
Cover(tr+s,tc+s,dr,dc,s);
}
}

void Print(int s)
{
for( int i= 1;i<=s;i++)
{
for( int j= 1;j<=s;j++)
printf( “%5d “,Board[i][j]);
printf( “\n”);
}
}

int main()
{
int s= 1,k,x,y;
printf( “输入2残缺棋盘的规模:2^k,k=”);
scanf( “%d”,&k);
for( int i= 1;i<=k;i++)
s*= 2;
printf( “输入棋盘残缺位置(x,y):”);
scanf( “%d%d”,&x,&y);
Board[x][y]= 0;
Cover( 1, 1,x,y,s);
Print(s);
return 0;
}
  
  

            </div>

4.归并排序
归并排序是一个利用分治算法的排序算法，其平均速度能达到nlogn是一个非常不错的排序算法。归并排序的主要步骤是分割和归并。
伪码：