2020牛客暑期多校训练营（第六场）Grid Coloring

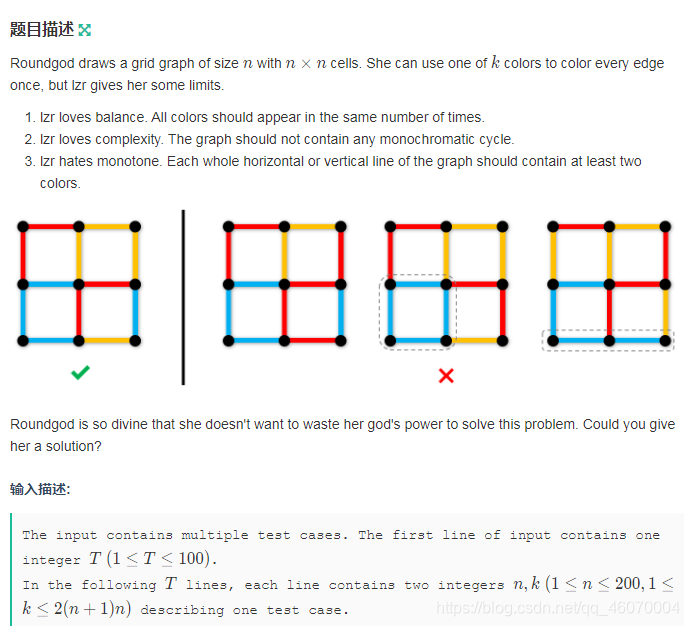
题目描述

分析

先判断无解的情况，易得：当 $n=1$， $k=1$， $2(n+1)n\%k≠0$时无解。
然后开始构造答案。由于是special judge，所以可以随便构造。
以下是一种方法：
我们可以把每一条边从上到下，从左到右标号，然后按 $1 \sim k$的顺序标号。
接下来证明为什么可行

1、

对于每一行和每一列，显然不会一种颜色到底，且每种颜色的出现次数相同

2、

对于每个1*1的环，相对的两条纵边必然不为同色，可行

3、

对于任意一个 $a(a+b),b>0$的环，横向边必定有相邻序号，所以染的颜色必然不同，由此又可以证明所有的横向边都是异色的。
对于任意一个 $(a+b)a,b>0$的环，如果他的横向边长为 $1$，那么他就有相邻的纵向边，如果他的横向边 $>1$那么他就有相邻横向边。
所以任意一个环和横边均异色。

4 、

然后观察上图，发现：任意两条相邻纵向边的序号差必定为 $2n+1$。
推理到这一步，我们只要证明任意两条相邻纵向边必定异色即可，
即 $gcd(k,2n+1)=1$，也就是 $gcd(2n(n+1),2n+1)=1$。
根据辗转相除法，容易求得原式等价于 $gcd(n,n+1)=1$
得证。
$\therefore$此种排色法可行
具体构造代码

		for (i=1;i<=n;i++)
		{
			for (j=1;j<=n;j++)
			 {
			 	l=l%k+1;
			 	a[i][j]=l;
			 }
			for (j=1;j<=n+1;j++)
			 {
			 	l=l%k+1;
			 	b[j][i]=l;
			 }
		}
		for (i=1;i<=n+1;i++)
		 {
		 	l=l%k+1;
		 	a[n+1][i]=l;
		 }

然后补全代码即可AC。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll n,m,i,j,k,l,o,p,a[250][250],b[250][250];
int main()
{
	ll T;
	for (scanf("%lld",&T);T--;)
	{
		l=0;
		scanf("%lld%lld",&n,&k);
		if (n==1 || k==1 || (n+1)*n*2%k) 
		{
			puts("-1");
			continue;	
		}
		for (i=1;i<=n;i++)
		{
			for (j=1;j<=n;j++)
			 {
			 	l=l%k+1;
			 	a[i][j]=l;
			 }
			for (j=1;j<=n+1;j++)
			 {
			 	l=l%k+1;
			 	b[j][i]=l;
			 }
		}
		for (i=1;i<=n+1;i++)
		 {
		 	l=l%k+1;
		 	a[n+1][i]=l;
		 }
		for (i=1;i<=n+1;i++)
		{
		 for (j=1;j<=n;j++)
		  printf("%lld ",a[i][j]);
		 printf("\n");		
		}
		for (i=1;i<=n+1;i++)
		{
		 for (j=1;j<=n;j++)
		  printf("%lld ",b[i][j]);
		 printf("\n");		
		}
	}
}