随机事件
随机事件的概念
随机试验E
- 试验可以在相同的条件下重复进行(重复性);
- 试验的可能结果不止一个,并且一切可能的结果都已知(多样性);
- 在每次试验前,不能确定哪一个结果会出现(随机性)。
样本空间S
- 随机试验E的所有可能结果组成的集合称为试验的样本空间
随机事件
- 随机试验E的样本空间S的子集称为E的随机事件
随机事件的关系
- 包含关系:B⊂A(B发生必导致A发生)
- 相等关系:B⊂A且A⊂B,则A=B
- 事件的和:A∪B(事件A发生或B发生,即A和B中至少有一发生)
- 事件的积:A∩B=AB(事件A发生且事件B发生)
- 事件的差:A-B(事件A发生且事件B不发生)
- 互不相容(互斥关系):A∩B=Ø(事件A和事件B不可能同时发生)
- 互逆关系(对立关系):若A∪B=S且A∩B=Ø,记为A=
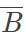 或B=
或B=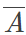
运算规律
- 交换律:A∪B=B∪A;A∩B=B∩A;
- 结合律:A∪(B∪C)=(A∪B)∪C;A∩(B∩C)=(A∩B)∩C
- 分配率:A∪(B∩C)=(A∪B)∩(A∪C);A∩(B∪C)=(A∩B)∪(A∩C)
- 对偶律:
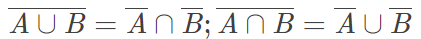
- P(A∪B)=P(A)+P(B)-P(AB)(如果A、B互斥,则P(AB)=0)
- P(A-B)=P(A)-P(AB)(若B⊂A,则P(AB)=P(B))
- P(A)=1-P(
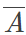 );P(A)=P(A
);P(A)=P(A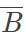 )+P(AB)
)+P(AB)
古典概率模型
- 试验的样本空间只含有有限个样本点,即基本事件数有限;
- 在每一次试验中,每个基本事件发生的可能性都相同。
- 古典概率P(A) = A中的基本事件 / S中包含的基本事件
排列Anm:从n个人中,有顺序地抽出m个人的抽法数;Anm=n(n-1)...(n-m+1)
组合Cnm:从n个人中,不计顺序地抽出m个人的抽法数;Cnm=n!/m!(n-m)!
条件概率、全概率公式与贝叶斯公式
条件概率
- 在事件A发生的条件下,事件B发生的条件概率:P(B|A)=P(AB)/P(A);P(B|A)=1-P(
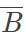 |A)
|A) - 乘法公式:若P(A)>0,则有P(AB)=P(A)P(B|A)
- 假如事件A与B相互独立,则P(AB)=P(A)P(B)
全概率公式
- 全概率就是表示达到某个目的,有多种方式(或者造成某种结果,有多种原因),问达到目的的概率是多少(造成这种结果的概率是多少)?
- P(A)=P(B1)P(A|B1)+P(B2)P(A|B2)+...+P(Bn)P(A|Bn)
贝叶斯公式
- 当已知结果,问导致这个结果的第i原因的可能性是多少?执果索因!

事件独立性和贝努利试验
事件独立性
- 事件B的发生与否,并没有影响到事件A发生的概率
- P(A|B)=P(A),即P(AB)=P(A)P(B)
贝努利试验
- 在同样的条件下重复地、相互独立地进行的一种随机试验,其特点是该随机试验只有两种可能结果:发生或者不发生。我们假设该项试验独立重复地进行了n次,那么就称这一系列重复独立的随机试验为n重贝努利试验。
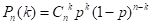 (P(A)=p,事件A恰好发生k次的概率)
(P(A)=p,事件A恰好发生k次的概率)
事件的独立和事件互斥两个概念的区别
1.互不相容考虑的是事件能否同时发生。A和B互斥:A发生B就不可能发生,B发生A就不可能发生,也就是说A和B不能同时发生。
2.事件的独立性考虑的是两个事件的关联性,一个事件的发生能否影响另一个事件。A和B独立:A发生和B发生没有关系,A发生不会影响B发生,但A和B也可能同时发生。