P2303 [SDOI2012] Longge 的问题
题意:求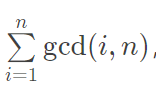
推式子
∑ i = 1 n g c d ( i , n ) ∑ d ∣ n d ∑ i = 1 n [ g c d ( i , n ) = d ] ∑ d ∣ n d ∑ i = 1 n d [ g c d ( i , n d ) = 1 ] ∑ d ∣ n d ϕ ( n d ) \sum_{i=1}^ngcd(i,n)\\ \sum_{d|n}d\sum_{i=1}^n[gcd(i,n)=d]\\ \sum_{d|n}d\sum_{i=1}^{\frac{n}{d}}[gcd(i,\frac{n}{d})=1]\\ \sum_{d|n}d\phi(\frac{n}{d})\\ i=1∑ngcd(i,n)d∣n∑di=1∑n[gcd(i,n)=d]d∣n∑di=1∑dn[gcd(i,dn)=1]d∣n∑dϕ(dn)
第一个式子:题目。
第二个式子:我们加一个枚举,枚举n的因子d(因为 g c d ( i , n ) gcd(i,n) gcd(i,n)一定是d的因子),然后统计 [ 1 , n ] [1,n] [1,n]中有多少个 g c d ( i , n ) = d gcd(i,n)=d gcd(i,n)=d,乘起来就是这个d对答案的贡献,把每个d算一遍,就是答案了。
第三个式子:我们可以这样理解 g c d ( i , n ) = d , 等 价 于 g c d ( i d , n d ) = 1 gcd(i,n)=d,等价于gcd(\frac id,\frac nd)=1 gcd(i,n)=d,等价于gcd(di,dn)=1,也就是我们可以在 [ 1 , n / d ] [1,n/d] [1,n/d]枚举 i i i,判断有多少个 g c d ( i , n d ) = 1 gcd(i,\frac nd)=1 gcd(i,dn)=1等价于在 [ 1 , n ] [1,n] [1,n]枚举 i i i判断有多少个 g c d ( i , n ) = d gcd(i,n)=d gcd(i,n)=d。
第四个式子:欧拉函数的定义。
Code
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll phi(ll x) {
//根据欧拉函数的性质,求欧拉函数值
ll n = x, res = x;
if(x == 1 || x == 2) return 1;
for(ll i=2; i*i<=x; i++) {
if(n % i == 0) {
res = res/i*(i-1);
while(n % i == 0) n /= i;
}
}
if(n > 1) res -= res/n;
return res;
}
int main() {
ll n, ans = 0;
cin >> n;
for(ll i=1; i*i<=n; i++) {
//枚举n的每个因子
if(n % i == 0) {
ans += phi(i)*(n/i);
//如果i*i != n,i和n/i就不相等了,就可以都加起来,不然的话只能加一遍。
if(n/i != i) ans += phi(n/i)*i;
}
}
cout << ans;
return 0;
}