声明:本FFT是针对OI的。专业人员请出门左拐。
Ⅰ前言
很久以前,我打算学习FFT。
然而,算法导论讲的很详细,却看不懂。网上博客更别说了,什么频率之类的都来了。我暗自下了决心:写一篇人看得懂的FFT
今天讲了FFT,我对这精(xuan)妙(xue)的算法有了初步的认识。我想,我如愿以偿了。
由于此算法不好理解的主要原因是涉及大量数学知识,所以我会尽量讲的浅显一点,以会写代码为目的。部分高超的证明会略去。
Ⅱ算法简介
快速傅里叶变换,FFT(Fast-Fast TLE,Fast Fourier Transform),是一种高效的多项式系数点值互换的算法(不懂没关系,一会儿要讲)。最广泛的应用是计算多项式乘法。
通常,暴力展开复杂度为O($n^{2}$)。而FFT则可以达到O(nlogn)
辣么我们开始吧。
Ⅲ前置知识(顺便简单提一下流程,后面流程详细讲)
1.多项式
回忆一下初中多项式的定义:
由若干个单项式相加组成的代数式叫做多项式。
单项式又是啥?
由数或字母的积组成的代数式叫做单项式。
low爆了!
我们已经是高中生了什么时候的事我怎么不知道,我们换一种定义:
多项式 := f(x)=$\sum_{i=0}^{n-1}a_{i}x^{i}\qquad$
其中n称为次数。
怎么样?有没有莫比乌斯反演的既视感?
2.多项式的表示方法
上面提到的叫做系数表达式。其实多项式还有一种表示:点值表达式。
标准定义找不到啊qwq
那这么说吧:
先把多项式看做一个函数,画出它的图像

然后在上面任取n个不同的点

那么这三个点就可以唯一的确定这个多项式。至于为什么唯一,通过意识流很容易证明。
为什么要引入这个东西呢?因为如果把两个多项式转换为x相同的点值,就可以O(n)求出它们的乘积。太神奇啦!
辣么现在问题就成了:如何把原多项式转成点值,再把乘出来的点值转系数。
最直观的方法:把原多项式转成点值就取几个值,点值转系数可以高斯消元。
于是尴尬的事情发生了:

总复杂度O($n^{3}$)
看来还要想办法啊。
3.弧度制和任意三角函数(学过的往后跳)
初中的三角函数是针对锐角的。那其他角有没有三角函数呢?
当然啦。
这要从任意角说起。
高中我们定义角为一条射线(一般指x正半轴)逆时针旋转后(称为终边)与原来的射线形成的图形,允许有负数,即顺时针
所以,这是个角:
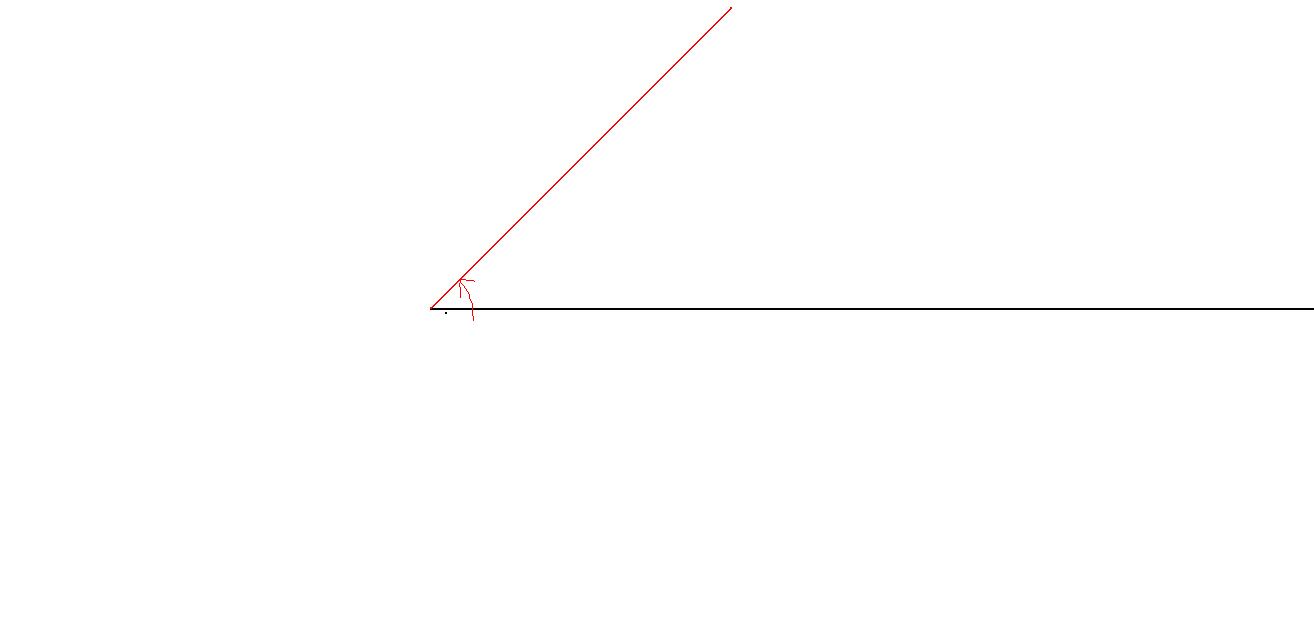
这也是个角,而且和上一个不同:

这还是个角,而且是负角:
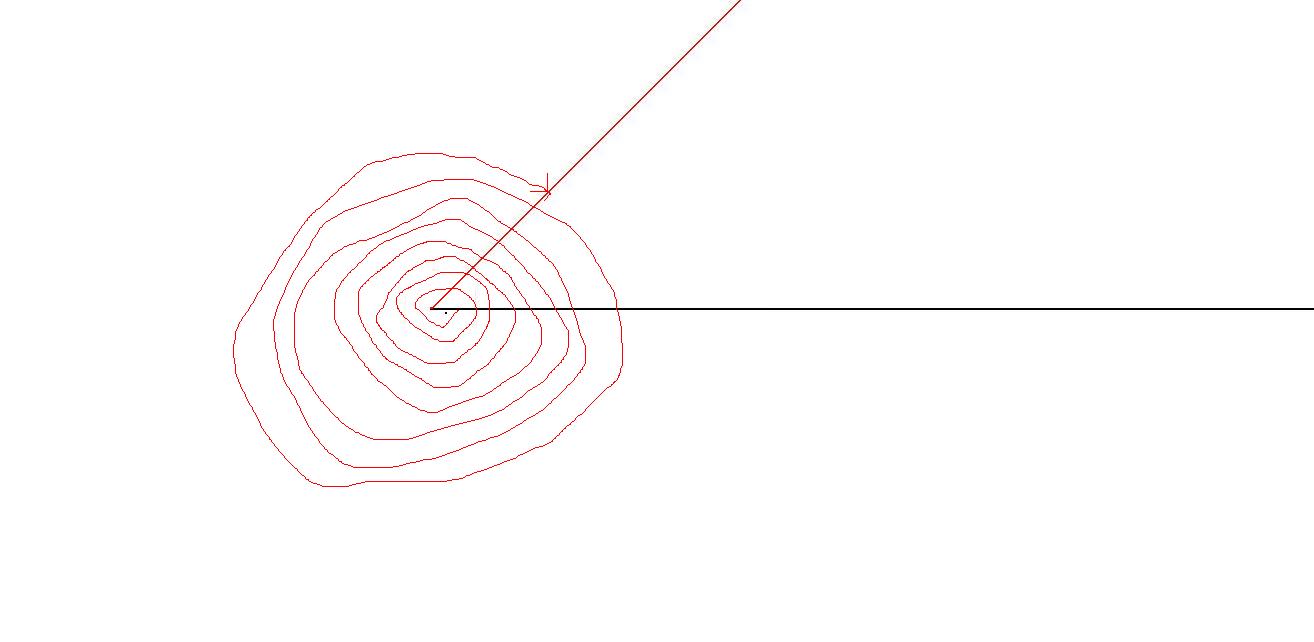
这仍然是个角:

好吧。。。
以前用角都是有单位,即1°=一个周角的1/360
那能不能换一个没单位的呢?
定义弧度为这个角所对弧长与半径的比,这样角就是一个常数。
很容易知道,一个周角是2π弧度。即π弧度对应180°。(前面那个是圆周率 垃圾markdown)
这样任意角三角函数就出来了:
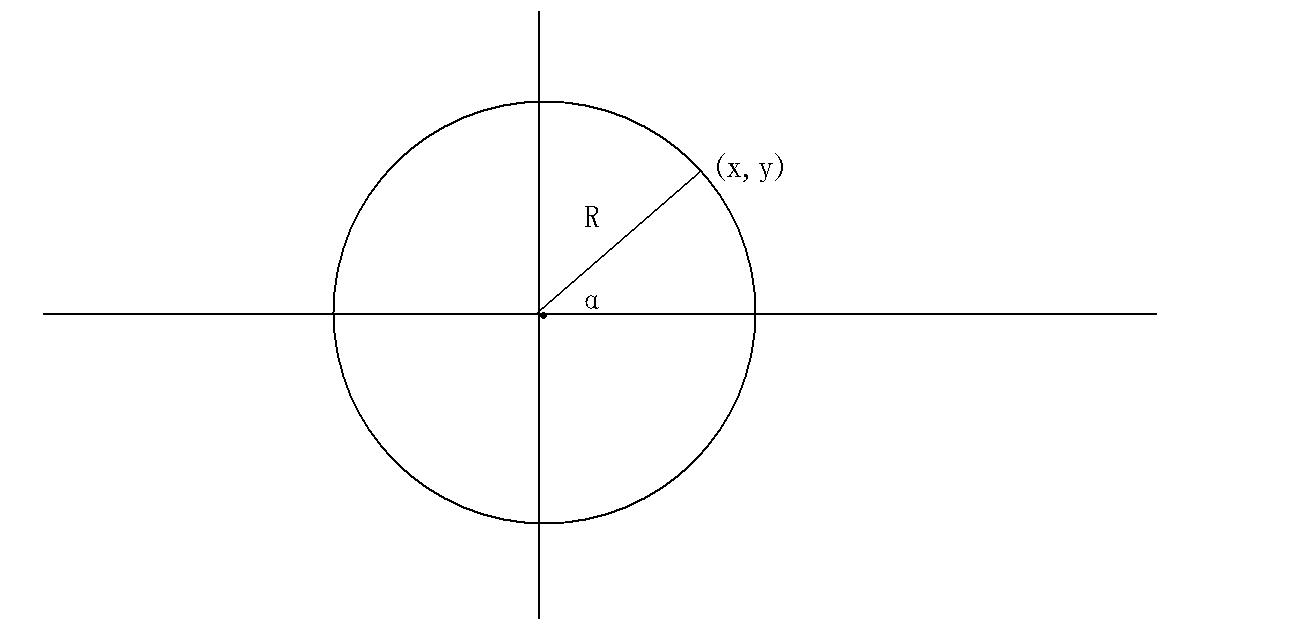
在直角坐标系中,以O为圆心作一个半径为R的圆。角α的终边与圆的交点坐标(x,y),那么有
sinα=$\frac{x}{R}$
cosα=$\frac{y}{R}$
其他三角函数类似,但FFT用不到,就不说了
4.复数与单位根
实数貌似没什么特殊性质。那实数之外呢?
我们定义$i^{2}$=-1。任何复数(也就是目前的所有数)都可以表示成x+yi的形式(x,y均为实数)
等等!这不是没有意义吗?这是什么鬼玩意儿?
好吧,你可以不管它。就把它看成这个:
1 struct complex 2 { 3 double x,y; 4 };
就好了。
当然它的乘法就是把它拆开,$i^{2}$换成-1,i保留就好了。(不懂没关系,后面看代码)
由于是两个实数,所以我们可以yy出一个平面:x代表实部,y代表虚部。这上面的点都是与复数一一对应的。
单位根就是满足$w^{n}$=1的所有复数,共n个,记为$w_{n}$(注:这里的w应该是个希腊字母,但为了偷懒就用w代替)
根据意识流在复平面上,这n个点与原点连线长度相同,且平分圆周。
并且,它们是$w_{n}$,$w_{n}^{2}$,$w_{n}^{3}$......$w_{n}^{n}$的关系,我们就这么表示好了
你可以用上面的性质把n个单位根算出来
即$w_{n}^{k}$=cos$\frac{2πk}{n}$+sin$\frac{2πk}{n}$i
Ⅳ算法流程
我们假装n是2的k次幂 即$n=2^{k}$,k为非负整数
令x=$w_{n}^{k}$,代入多项式
(注:1.如果你不想看,并且你可以在不理解的情况下背代码,可以跳过以下推导 2.以下的i都是循环变量而不是虚数单位)
$F(w_{n}^{k})=\sum_{i=0}^{n-1}a_{i}w_{n}^{ik}$
闲着没事,把它按奇偶分类:
$F(w_{n}^{k})=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}w_{n}^{2ik}+a_{2i+1}w_{n}^{(2i+1)k}$
看后面那坨不顺眼
$F(w_{n}^{k})=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}w_{n}^{2ik}+w_{n}^{k}a_{2i+1}w_{n}^{2ik}$
根据折半引理:
$(w_{n}^{k})^{2}=w_{\frac{n}{2}}^{k}$
可得:
$F(w_{n}^{k})=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}w_{\frac{n}{2}}^{ik}+w_{n}^{k}a_{2i+1}w_{\frac{n}{2}}^{ik}$
有没有一种似曾相识的感觉呢?
所以可以递归下去:(type干啥的马上就知道了)
const double PI=acos(-1.0); struct complex { double x,y; complex(double x=0,double y=0):x(x),y(y){} }a[MAXN],b[MAXN]; complex operator +(const complex& a,const complex& b){return complex(a.x+b.x,a.y+b.y);} complex operator -(const complex& a,const complex& b){return complex(a.x-b.x,a.y-b.y);} complex operator *(const complex& a,const complex& b){return complex(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);} void fft(int lim,complex *a,int type) { if (lim==1) return; complex a1[lim>>1],a2[lim>>1]; for (int i=0;i<=lim;i+=2) a1[i>>1]=a[i],a2[i>>1]=a[i+1]; fft(lim>>1,a1,type); fft(lim>>1,a2,type); complex wn(cos(2.0*PI/lim),type*sin(2.0*PI/lim)),w(1,0); for (int i=0;i<(lim>>1);i++,w=w*wn) { a[i]=a1[i]+w*a2[i]; a[i+(lim>>1)]=a1[i]-w*a2[i]; } }
于是 就完了?
怎么可能?
上面只是系数转点值。而平时点值很少用,即使用也不会是复数啊……
所以还要把点值转系数。我们称为傅里叶逆变换。
又是推式子的时间啦!
(其实这里我也不怎么懂……但结论很简单,直接记就行)
我们设$c_{i}$为多项式在$w_{n}^{-i}$的点值表达式(也就是y值),其中$0<=i<n$LaTeX可以美化呢
即
$c_{k}=\sum_{i=0}^{n-1}y_{i}(w_{n}^{-k})^{i}$
把$y_{i}$拆开
$=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_{j}(w_{n}^{i})^{j})(w_{n}^{-k})^{i})$
你到前面来
$=\sum_{i=0}^{n-1}(\sum_{j=0}^{n-1}a_{j}(w_{n}^{j})^{i})(w_{n}^{-k})^{i})$
辣眼睛的小括号
$=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_{j}(w_{n}^{j})^{i}(w_{n}^{-k})^{i}$
咦?
$=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}a_{j}(w_{n}^{j-k})^{i}$
瞎搞一波
$=\sum_{i=0}^{n-1}a_{j}(\sum_{j=0}^{n-1}(w_{n}^{j-k})^{i})$
设$S(x)=\sum_{i=0}^{n-1}x$
代入
$S(w_{n}^{k})=1+(w_{n}^{k})+(w_{n}^{k})^{2}+... ... +(w_{n}^{k})^{n-1}$
当k不为0时,运用你丰富的等比数列知识
$S(w_{n}^{k})=\frac{(w_{n}^{k})^{n}-1}{(w_{n}^{k})-1}$
$S(w_{n}^{k})=0$
k=0时,显然$S(w_{n}^{k})=n$
手贱点了发布。。。正在赶,有缘看到可以等一下