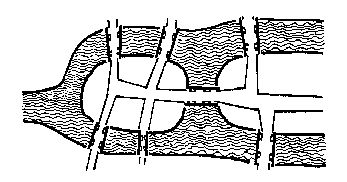
哥尼斯堡是位于普累格河上的一座城市,它包含两个岛屿及连接它们的七座桥,如下图所示。
可否走过这样的七座桥,而且每桥只走过一次?瑞士数学家欧拉(Leonhard Euler,1707—1783)最终解决了这个问题,并由此创立了拓扑学。
这个问题如今可以描述为判断欧拉回路是否存在的问题。欧拉回路是指不令笔离开纸面,可画过图中每条边仅一次,且可以回到起点的一条回路。现给定一个无向图,问是否存在欧拉回路?
输入格式:
输入第一行给出两个正整数,分别是节点数N (1≤N≤1000)和边数M;随后的M行对应M条边,每行给出一对正整数,分别是该条边直接连通的两个节点的编号(节点从1到N编号)。
输出格式:
若欧拉回路存在则输出1,否则输出0。
输入样例1:
6 10
1 2
2 3
3 1
4 5
5 6
6 4
1 4
1 6
3 4
3 6
输出样例1:
1
输入样例2:
5 8
1 2
1 3
2 3
2 4
2 5
5 3
5 4
3 4
输出样例2:
0原理及定义:
欧拉回路:图G,若存在一条路,经过G中每条边有且仅有一次,称这条路为欧拉路,如果存在一条回路经过G每条边有且仅有一次,
称这条回路为欧拉回路。具有欧拉回路的图成为欧拉图。
判断欧拉路是否存在的方法
有向图:图连通,有一个顶点出度大入度1,有一个顶点入度大出度1,其余都是出度=入度。
无向图:图连通,只有两个顶点是奇数度,其余都是偶数度的。
判断欧拉回路是否存在的方法
有向图:图连通,所有的顶点出度=入度。
无向图:图连通,所有顶点都是偶数度。
1.凡是由偶点组成的连通图,一定可以一笔画成。
2.凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。
3.其他情况的图都不能一笔画出。
思路:知道了上面的只是, 我们先用并查集判断所给的图是否连通,不连通一定不是欧拉回路;
步骤:
1】利用并查集判断是否连通(其实最后就是看是不是有独立的一个点的情况,并且这种点 >1 的时候一定不连通);
2】在利用并查集的时候,可以直接把两个点存进对方的数组里面(因为最后会判断每个点的奇偶,也就是与几个点联通)。
3】利用1】、2】就可以得到每个点的奇偶值,也可以知道与谁连通;我们只需要按照原理判断即可(就是看如果有大于一个点的值是-1的话,说明有多于1个点的独立点,那么一定不连通;若一共就一个点,那么连通;否则,一定只有一个是-1的点);
#include<iostream>
#include<vector>
#include<cstdio>
using namespace std;
#define MAX 10005
vector<int> v[MAX];//用于存放每个点与那个点连接
int pre[MAX]; //并查集数组,后面我们初始化为-1,为-1时就意味着查到老祖宗了^_^!
int Find(int x){ //并查集搜索
if(pre[x] == -1)
return x;
else
return pre[x] = Find(pre[x]);
}
void Join(int x,int y){ //并查集连接
int fx = Find(x);
int fy = Find(y);
if(fx != fy){
pre[fy] = fx;
}
}
int main(){
int N,M;
scanf("%d%d",&N,&M);
memset(pre,-1,sizeof(pre)); //并查集数组初始化
for(int i = 0; i <= N; i++) //清空数组
v[i].clear();
int a,b;
for(int j = 0; j < M; j++){ //输入
scanf("%d%d",&a,&b);
Join(a,b); //连接
v[a].push_back(b); //把对方分别放进自己的数组
v[b].push_back(a);
}
int count = 0,num = 0; //创建两个变量count用来统计奇数点(与其他点有奇数个连接), num用来统计自己只与自己连通的点的个数
for(int k = 1; k <= N; k++){
if(v[k].size()%2){
count++;
}
if(Find(k) == k){
num++;
}
}
if(count == 0 && num == 1) //当都是偶数点,并且只有一个-1时,是欧拉回路
printf("1\n");
else //否则不是
printf("0\n");
/*<测试代码>
for(int m = 0;m<N;m++){
for(int n=0;n<v[m].size();n++){
cout<<v[m][n]<<" ";
}
cout<<endl;
}
cout<<endl;
for(int l=0;l<N;l++){
cout<<pre[l]<<" ";
}
*/
return 0;
}