http://kjwy.5any.com/gdsx22/other/kcjg/index.htm
第七章 向量代数与空间解析几何
§7.1 空间直角坐标系
7.1.1 空间点的直角坐标系
过空间一个定点O，作三条互相垂直、具有相同的长度单位的数轴它们分别称为x轴、y轴和z轴，并使得它们的正向符合右手法则，即以右手握住z轴，当右手的四个手指从正向x轴，以
角度转向正向y轴时，大拇指的指向就是z轴的正向，如图7-1。
图中箭头的指向表示x轴、y轴、z轴的正向。这样的三条坐标轴就组成了一个空间直角坐标系。点O叫做坐标原点(或原点)。
三条坐标轴中的任意两条可以确定一个平面，这样定出的三个平面统称为坐标面。由x轴及y轴所确定的坐标面叫做xOy面，另两个由y轴及z轴和由z轴及x轴所确定的坐标面，分别叫做yOz面及zOx面。
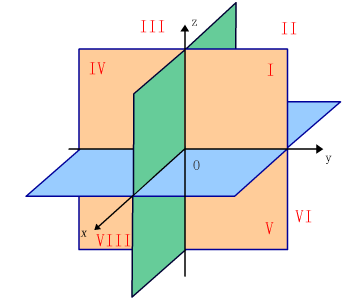
三个坐标面把空间分成八个部分，每一部分叫做卦限。含有x轴、y轴与z轴正半轴的那个卦限叫做第一个卦限，其它第二、第三、第四卦限，在xOy面的上方，按逆时针方向确定。第五至第八卦限，在xOy面的下方，由第一卦限之下的第五卦限，按逆时针方向确定，这八个卦限分别用字母I、II、III、IV、V、VI、VII、VIII表示。
7.1.2 点的坐标
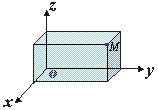
设M为空间一已知点。我们过点M作三个平面分别垂直于x轴、y轴和z轴，它们与x轴、y轴、z轴的交点依次为P、Q、R（图7-2），这三点在x轴、y轴、z轴上的坐标依次为x、y、z。于是空间的一点M就唯一地确定了一个有序数组x，y，z；反过来，已知一有序数组x，y，z，我们可以在x轴上取坐标为x的点P，在y轴上取坐标为y的点Q，在z轴上取坐标为z的点R，然后通过P、Q与R分别作x轴、y轴和z轴的垂直平面。这三个垂直平面的交点M便是由有序数组x，y，z所确定的唯一的点。这样，就建立了空间的点M和有序数组x，y，z之间的一一对应关系。这组数x，y，z就叫做点M的坐标，并依次称x，y和z为点M的横坐标，纵坐标和竖坐标。坐标为x，y，z的点M通常记为M(x,y,z)。
在坐标面上与坐标轴上的点有其特性，具体的说：
- 如果点M在yOz面上，则在点M的坐标中x=0；点M在zOx面上，则在点M的坐标中y=0；点M在xOy面上，则在点M的坐标中z=0。即在坐标面上的点的坐标特点是：点在哪根坐标面上，点的哪个坐标为零。如xoy面的方程为
，则xoy面上的点是
。 - 如果点M在x轴上，则在点M的坐标中y=z=0；点M在y轴上，则在点M的坐标中z=x=0；点M在z轴上，则在点M的坐标中x=y=0。即在坐标轴上的点的坐标特点是：点在哪根坐标轴上，则哪个坐标非零，而点的另外两个坐标为零。
- 如果点M为原点，则x=y=z=0。
7.1.3 空间两点间的距离
设
、
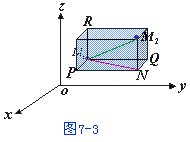
为空间两点，为了用两点的坐标来表达它们之间的距离d，我们过M1、M2各作三个分别垂直于三条坐标轴的平面。这六个平面围成一个以M1M2为对角线的长方体（图7-3）。
由于
为直角，
为直角三角形，所以
又 
也是直角三角形，且
，所以
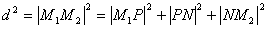
由于
，
，
，
所以
这就是空间两点间的距离公式。
特殊地，点
与坐标原点
的距离为
例1：求两点
与
的距离。
解：
例2：求证以
、
、
三点为顶点的三角形是一个等腰三角形。
分析：要证明一个三角形是等腰三角形，只要证明在该三角形中有两条边相等方可，由于给出了三个点的坐标，因此用两点间的距离公式解决。
解：
例3：设P在x轴上，它到
的距离为到点
的距离的两倍，求点P的坐标。
分析：由假设有：
2
注意到点P在X轴上，由在坐标轴上的点的特点，
可设点P的坐标为（x，0，0）。
利用两点间距离公式方可求出点P的坐标。
解：
思考题
1、写出点P（a，b，c）关于坐标面、坐标轴、原点的对称点的坐标。
解：关于XOY面的对称点
 |
关于YOZ面的对称点
 |
关于ZOX面的对称点
 |
关于X轴的对称点
 |
关于Y轴的对称点
 |
关于Z轴的对称点
 |
关于原点对称点
 |
2、过点
分别作平行于z轴的直线和平行于xOy面的平面，问在它们上面的点的坐标各有什么特点？