B站网课——开环系统Nyquist曲线绘制

2020-04-16 5.2开环系统Nyquist曲线绘制

绘制方法

1. 解析法

对于开环传递函数$G(s)H(s)$，令$s=j\omega$，得到开环系统的频率特性$G(j\omega )H(j\omega )$（一定是一个复变函数），令$\omega$在$(0,+\infty )$取值、列表、描点、连线。（工程实践中不适用）。

2. 借助软件绘制

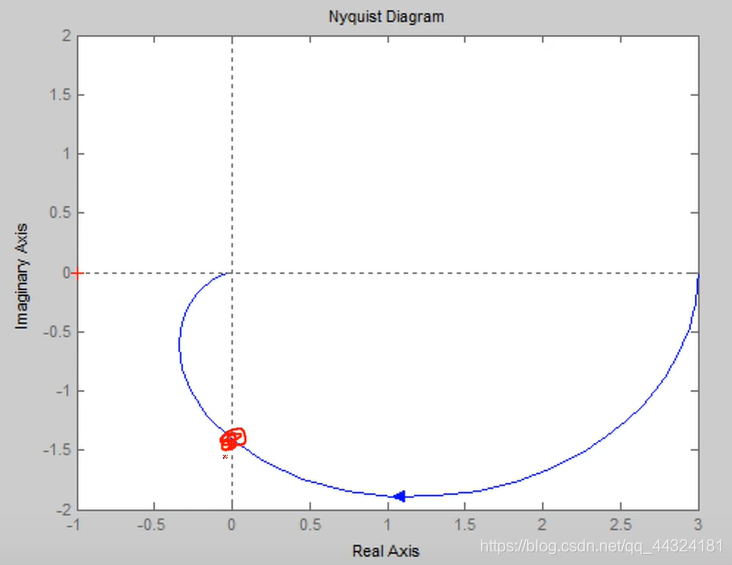
G1 = tf([2 5], [1 4 3 0]);
nyquist(G1);

3. 典型环节绘制法

3.0 过程

• 典型环节相乘时，幅值相乘、相角相加
• 绘制的是概略地 Nyquist 曲线（把核心要素绘制准确）
  

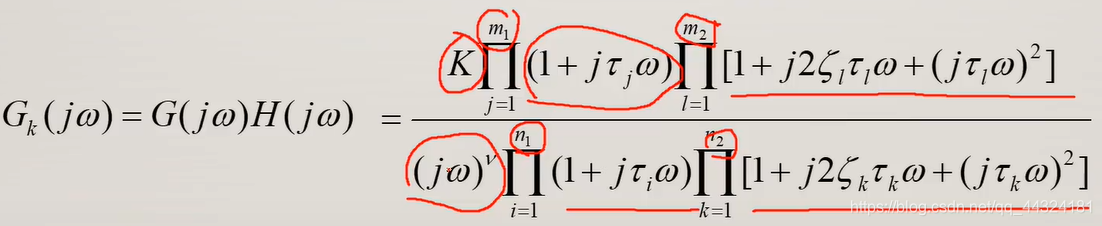
3.1 Nyquist曲线的起点 $\omega =0_{+}$

开环频率特性转化为
$$G(j\omega )H(j\omega )\to \frac{K}{(j\omega {)}^{\nu }}$$
因此起点与比例环节$K$和积分环节的个数有关。

• $\nu <0$，起于原点，幅值为$0$，相角为$-\nu \cdot 90°$
• $\nu =0$，没有积分环节，幅值为$K$，相角为$0°$，起于$(K,j0)$
• $\nu >0$，有$\nu$个积分环节，幅值为$\infty$，相角为$-\nu \cdot 90°$
  • 若起于虚轴附近的无穷远处（积分环节为奇数），则看实部在$\omega =0_{+}$的极限值，
    • 若为正，则起于虚轴右侧；
    • 若为负，则起于虚轴左侧；
    • 若为0，则起于虚轴上。
  • 若起于实轴附近的无穷远处（积分环节为偶数），则看虚部在$\omega =0_{+}$的极限值，
    • 若为正，则起于实轴上方；
    • 若为负，则起于实轴下方；
    • 若为0，则起于实轴上。

3.2 Nyquist曲线的终点($\omega \to \infty$)

• $n=m$，频率特性分子分母阶次相同，$\omega \to \infty$时，结果为$K^{\ast }$，终点为$(K^{\ast },j0)$。
• $n>m$，频率特性分母阶次大于分子阶次，$\omega \to \infty$时，幅值为$0$，相角为$(n-m)\times (-90°)$，终点是原点，按照$(n-m)\times (-90°)$趋近于终点。

3.3 Nyquist曲线与虚轴的交点

令频率特性实部为$0$，求出自变量频率$\omega$的值，再带入到频率特性虚部当中，即可求出曲线与虚轴交点坐标。

3.4 Nyquist曲线与实轴的交点

令频率特性虚部为$0$，求出自变量频率$\omega$的值，再带入到频率特性实部当中，即可求出曲线与实轴交点坐标。

3.5 典型环节绘制法绘制步骤

1. 根据规律1、2判断起点和终点的大体位置；
2. 可根据典型环节的规律判断象限；
3. 根据规律3、4确定与实轴和虚轴的交点；
4. 画出概略开环幅相特性图。

3.6 例题

例1
已知系统的开环传递函数
$$G(s)=\frac{K}{(T_{1}s+1)(T_{2}s+1)},(K,T_1,T_2>0)$$
实概略绘制系统开环幅相曲线。

---

解：

• $0^{\circ },(0,-90^{\circ }),(0,-90^{\circ })$总的为$(0,-180^{\circ })$
• 起点：$\nu =0$，起于$(K,j0)$点，$A(0)=K,\varphi (0)=0^{\circ }$
• 终点：与分母阶次$n$和分子阶次$m$有关，$n=2,m=0,n>m$，终点为原点，从$-180°$方向回到原点，$A(\infty )=0,\varphi (\infty )=-180^{\circ }$
• 其频率特性为：
  $$G(j\omega )=\frac{K-K{T}_1{T}_2{\omega }^2}{(1+T_1^2{\omega }^2)(1+T_2^2{\omega }^2)}+\frac{-jK(T_1+T_2)\omega }{(1+T_1^2{\omega }^2)(1+T_2^2{\omega }^2)}$$
• 与虚轴有交点，与实轴没有交点，令实部=0，解得$\omega$代入虚部，即得到与虚轴的交点。
  

例2
已知系统的开环传递函数
$$G(s)=\frac{K}{s(T_{1}s+1)(T_{2}s+1)},(K,T_1,T_2>0)$$
实概略绘制系统开环幅相曲线。

---

解：

• $0^{\circ },-90^{\circ },(0,-90^{\circ }),(0,-90^{\circ })$总的为$(-90^{\circ },-270^{\circ })$
• 起点：$\nu =1$，起于无穷远处，相角为$-90^{\circ }$
• 终点：与分母阶次$n$和分子阶次$m$有关，$n=3,m=0,n>m$，终点为原点，从$-270°$方向回到原点
• 它与实轴应该有一个交点
• 系统开环频率特性为
  $$G(j\omega )=\frac{-K(T_1+T_2)\omega }{\omega (1+T_1^2{\omega }^2)(1+T_2^2{\omega }^2)}-j\frac{K(1-T_1{T}_2{\omega }^2)}{\omega (1+T_1^2{\omega }^2)(1+T_2^2{\omega }^2)}$$
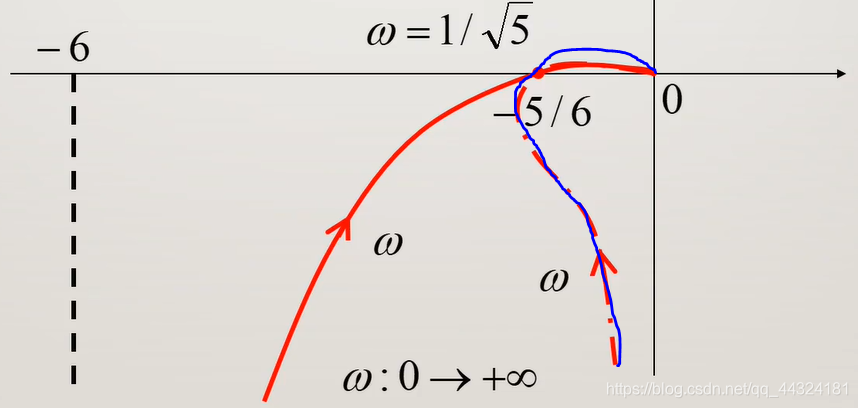
  • 实部为负，虚部可正可负可为0，故图像在第二、三象限
  • 当$\omega =0$时，$Re(G)=-K(T_1+T_2)$，故开环幅相曲线在$\omega =0$时，起点在第三象限，沿渐近线$Re(G)=-K(T_1+T_2)$从无穷远点起始
  • 令虚部=0，解得$\omega$，代入实部，得与实轴得交点
  • 当$\omega \to \infty$时，$Re(G)<0,Im(G)>0$，所以开环幅相曲线在$\omega \to \infty$时在第二象限沿正虚轴趋于原点。
    

对比例1和例2，，例2多了一个积分环节，所以曲线顺时针旋转$90^{\circ }$，又因为$\nu =1$，所以起点是无穷远处。

下一篇：Bode曲线的绘制