本课程来自
深度之眼,部分截图来自课程视频。
【第二章 微积分】2.2泰勒公式函数极值定积分
在线LaTeX公式编辑器
任务详解:
这节课主要介绍了泰勒公式,函数的凹凸性,函数的极值,不定积分,定积分等知识点。
掌握目标:
1、了解泰勒公式
2、了解函数的凹凸性
3、掌握函数的极值,以及极值的充要条件
4、掌握不定积分,定积分的计算,第一第二类换元,分部积分法,牛顿莱布尼茨公式
1.泰勒公式
泰勒(Taylor)中值定理1:如果函数
f(x)在
x0处具有n阶导数,那么存在
x0的一个邻域,对于该邻域内的任一
x,有
f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+...+n!fn(x0)(x−x0)n+Rn(x)
其中:
Rn(x)=o((x−x0)n)
说人话:这个定理就是任意一个函数
f(x),都可以在
x0展开,写成一个多项式的模式,最后一项就是误差
Rn(x),是x到
x0的高阶无穷小(佩亚诺余项)。
泰勒(Taylor)中值定理2:如果函数
f(x)在
x0的某个邻域
U(x0)内具有(n+1)阶导数,那么对任一
x∈U(x0),有
f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+...+n!fn(x0)(x−x0)n+Rn(x)
其中:
Rn(x)=(n+1)!fn+1(ξ)(x−x0)n+1
ξ是
x0与
x之间的某个值,这项也叫:拉格朗日余项
当×0=0时,称为麦克劳林展开
例子(略)
2.函数的凹凸性
定义:设
f(x)在区间
I上连续,如果对
I上任意两点
x1,x2恒有
f(2x1+x2)<2f(x1)+f(x2)
那么称
f(x)在
I上的图形是(向上)凹的(或凹弧);如果恒有
f(2x1+x2)>2f(x1)+f(x2)
那么称
f(x)在
I上的图形是(向上)凸的(或凸弧).
如果函数
f(x)在
I内具有二阶导数,那么可以利用二阶导数的符号来判定曲线的凹凸性,这就是下面的曲线凹凸性的判定定理:
定理2:设
f(x)在[a,b]上连续,在(a,b)内具有一阶和二阶导数,那么
(1)若在(a,b)内
fn(x)>0,则
f(x)在[a,b]上的图形是凹的;
(2)若在(a,b)内
fn(x)<0,则
f(x)在[a,b]上的图形是凸的.
证明:
设
x1和
x2为[a,b]类任意两点,且
x1<x2,记
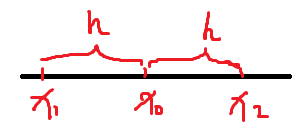
2x1+x2=x0,并记
x2−x0=x0−x1=h,则
x1=x0−h,
x2=x0+h
由拉格朗日中值公式可得:
f(x0+h)−f(x0)=f′(ξ1)(x0+h−x0)=f′(x0+θ1h)h,0<θ1<1(1)
f(x0)−f(x0−h)=f′(ξ2)(x0−x0+h)=f′(x0−θ2h)h,0<θ2<1(2)
上面由于
ξ1是在
x0到
x0+h之间的,所以可以写成最后那个样子
(ξ1=x0+θ1h是等价的,
ξ2同理。
等式(1)减(2)得:
f(x0+h)+f(x0−h)−2f(x0)=[f′(x0+θ1h)−f′(x0−θ2h)]h(3)
对等式(3)中的
f′(x0+θ1h)−f′(x0−θ2h)再来一次拉格朗
日
中值公式:
f′(x0+θ1h)−f′(x0+θ2h)=f′′(ξ3)(x0+θ1h−x0+θ2h)
=f′′(ξ3)(θ1+θ2)h(4)
将(4)带入(3):
f(x0+h)+f(x0−h)−2f(x0)=f′′(ξ3)(θ1+θ2)h2(5)
对于定理的第一种情况
(1)若在(a,b)内
fn(x)>0,则
f(x)在[a,b]上的图形是凹的;
我们可以由
f′′(ξ3)>0,(θ1+θ2)>0,h2>0,对公式(5)判断:整体大于0,即:
f(x0+h)+f(x0−h)−2f(x0)>0
把
x1=x0−h,
x2=x0+h,
2x1+x2=x0带回去
f(x2)+f(x1)>2f(2x1+x2)
证明完毕
f(2x1+x2)<2f(x1)+f(x2)
情况二类似。
3.函数的极值
定义设函数
f(x)在点
x0的某邻域
U(x0)内有定义,如果对于去心邻域
Uo(x0)内的任一x,有
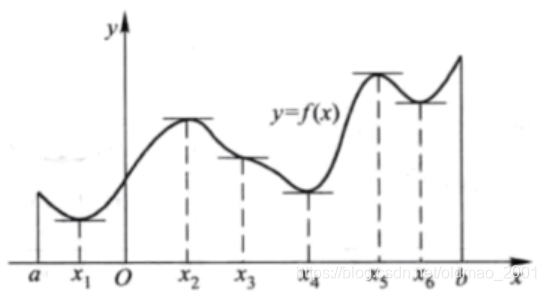
f(x)<f(x0)(或f(x)>f(x0))
说人话:就是
x0比附近所有的x的值都大(小)。
那么就称
f(x0)是函数
f(x)的一个极大值(或极小值).
定理1(必要条件):设函数
f(x)在
x0处可导,且在
x0处取得极值,则
f′(x)=0
定理2(第一充分条件):设函数
f(x)在
x0处连续,且在
x0的某去心邻域
Uo(x0,δ)内可导.
(1)若
x∈(x0−δ,x0)时,
f′(x)>0,而
x∈(x0,x0+δ)时,
f′(x)<0,则
f(x)在
x0处取得极大值;
说人话:在x的左边导数大于0(函数递增),右边导数小于0(函数递减).
(2)若
x∈(x0−δ,x0)时,
f′(x)<0,而
x∈(x0,x0+δ)时,
f′(x)>0,则
f(x)在
x0处取得极小值;
(3)若
x∈Uo(x0,δ)时,
f′(x)的符号保持不变,则
f(x)在
x0处没有极值。
定理3(第二充分条件):设函数
f(x)在
x0处具有二阶导数且
f′(x0)=0,
f′′(x0)=0,则
(1)当
f′′(x0)<0时,函数
f(x)在
x0处取得极大值;
(2)当
f′′(x0)>0时,函数
f(x)在
x0处取得极小值.
这个定理3是根据函数的凹凸性来进行判断了,也可以用泰勒展开式来进行判断。
4.不定积分(求原函数)
定义1:如果在区间
I上,可导函数
F(x)的导函数为
f(x),即对任一
x∈I,都有
F′(x)=f(x)或dF(x)=f(x)dx,那么函数F(x)就称为
f(x)(或f(x)dx)在区间
I上的一个原函数
定义2:在区间
I上,函数
f(x)的带有任意常数项的原函数称为
f(x)(或
f(x)dx)在区间
I上的不定积分,记作
∫f(x)dx
其中记号
∫称为积分号,
f(x)称为被积函数,
f(x)dx称为被积表达式,
x称为积分变量。
由此定义及前面的说明可知,如果
F(x)是
f(x)在区间
I上的一个原函数,那么
F(x)+C就是
f(x)的不定积分,即
∫f(x)dx=F(x)+C
性质1:设函数
f(x)及
g(x)的原函数存在,则:
∫[f(x)+g(x)]dx=∫f(x)dx+∫g(x)dx
性质2:设函数
f(x)的原函数存在,k为非零常数,则
∫kf(x)dx=k∫f(x)dx
第一类换元法(凑微分)
定理1:设
f(u)具有原函数,
u=φ(x)可导,则有换元公式
∫f[φ(x)]φ′(x)dx=[∫f(u)du]u=φ(x)
例子:求
∫2cos2xdx
∫2cos2xdx=∫cos2xd2x
令
u=2x
∫cos2xd2x=∫cosudu=sinu+C
带回
u=2x
∫2cos2xdx=sin2x+C
第二类换元法
定理2:设
x=ψ(t)是单调的可导函数,并且
ψ′(t)=0.又设
f[ψ(t)]ψ′(t)具有原函数,则有换元公式
∫f(x)dx=[∫f[ψ(t)]ψ′(t)dt]t=φ−1(x)
其中
φ−1(x)是
x=ψ(t)的反函数.
扫描二维码关注公众号,回复:
9488810 查看本文章

分部积分法
∫udv=uv−∫vdu
例子:求
∫xcosxdx
∫xcosxdx=∫xdsinx=xsinx−∫sinxdx=xsinx+cosx+C
5.定积分
定积分的意义:曲线的面积
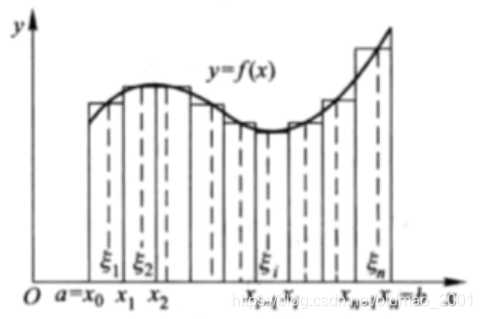
在区间[a,b]中任意插入若干个分点
a=x0<x1<x2<……<xn−1<xn=b
把[a,b]分成n个小区间
[x0,x1],[x1,x2],…,[xn−1,xn]
它们的长度依次为
Δx1=x1−x0,Δx2=x2−x1,...,Δxn=xn−xn−1
面积A为:
A≈f(ξ1)Δx1+f(ξ2)Δx2+...+f(ξn)Δxn=i=1∑nf(ξi)Δxi
其中
ξi是在
xi−1∼xi区间的任意一个值。
为了保证所有小区间的长度都无限缩小,我们要求小区间长度中的最大者趋于零,如记
λ=max∣Δx1,Δx2,…,Δxn∣,则上述条件可表示为
λ→0.当
λ→0时(这时分段数n无限增多,即
n→∞),取上述和式的极限,便得曲边梯形的面积
A=λ→0limi=1∑nf(ξi)Δxi
∫abf(x)dx=I=λ→0limi=1∑nf(ξi)Δxi
牛顿莱布尼茨公式
定理3(微积分基本定理)如果函数
F(x)是连续函数
f(x)在区间[a,b]
上的一个原函数,那么
∫abf(x)dx=F(b)−f(a)
换元法
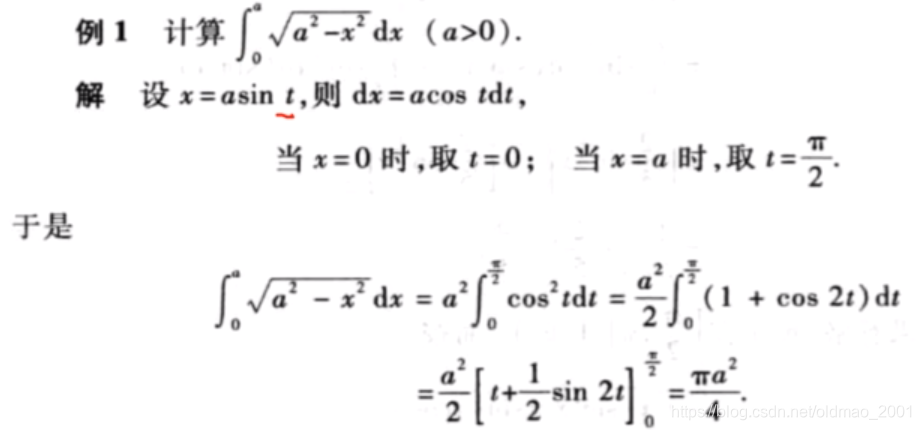
分部积分
例子:
∫01xe−xdx=∫01−xde−x=[−xe−x]01−∫01e−xd−x
=(−1e−1)−∫10eudu=−e−1−[eu]10=e−1−1+e