FFT快速傅里叶变换（超详细的入门学习总结）

FFT快速傅里叶变换

说明

• 本文创作的目的是为自己巩固该算法，加深印象并深入理解，同时也为FFT入门学者提供一份可鉴的学习总结。
• 原文链接：https://blog.csdn.net/qq_39565901/article/details/94648221
• 版权归作者所有，允许参考，转载需注明作者。

参考&鸣谢

小学生都能看懂的FFT！！！
十分简明易懂的FFT（快速傅里叶变换）
浅谈 FFT （终于懂一点了~~）
数学黑科技1——FFT

什么是FFT？

• FFT（Fast Fourier Transformation） 是离散傅氏变换（DFT）的快速算法。即为快速傅氏变换。它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。——百度百科
• 这是什么并不重要。。。

用来做什么？

• 标准的FFT模板题，
• 设两个多项式：
• $A=\sum_{i=0}^na_i*x^i=a_n*x^n+a_{n-1}*x^{n-1}+...+a_1*x+a_0$，
• $B=\sum_{i=0}^mb_i*x^i=b_n*x^m+b_{m-1}*x^{m-1}+...+b_1*x+b_0$，
• 求 $A*B$的值？
• 难道不就是 $Ans=\sum_{i=0}^{n+m}s_i*x^i=\sum_{i=0}^{n+m}\sum_{j=0}^{i}a_j*b_{i-j}*x^i$
• 是的，用 $A$的每一项和 $B$的每一项分别相乘，时间复杂度 $O(nm)$.
• 但如何跑得更快呢？
• ——用FFT！
• 经典的应用，
• 高精度乘法（是不是十分显然）。

关于多项式

• 上面的多项式表示法是最普通的，也就是平时课本上看到的，称为“系数表示法“，因为显而易见每一项的系数分别是多少。
• 现在介绍另一种表示法——“点值表示法”，
• 一个 $n$次 $n+1$项式，可以将其看做是 $n$次函数的解析式，
• 为了唯一确定这个 $n$次多项式，需要选取 $n+1$个不同的 $x$代入该式子，分别得到一个对应的 $y$，
• 也就是，
• $a_n*x_0^n+a_{n-1}*x_0^{n-1}+...+a_1*x_0+a_0=y_0$，
• $a_n*x_1^n+a_{n-1}*x_1^{n-1}+...+a_1*x_1+a_0=y_1$，
• $……$
• $a_n*x_n^n+a_{n-1}*x_n^{n-1}+...+a_1*x_n+a_0=y_n$，
• 那么就有两个多项式分别表示为（注意要取相同的且个数相同的 $x$），
• $A=((x_0,{y_A}_0)),(x_1,{y_A}_1),...,(x_n,{y_A}_n))$
• $B=((x_0,{y_B}_0)),(x_1,{y_B}_1),...,(x_n,{y_B}_n))$
• 则它们的积为，
• $Ans=((x_0,{y_A}_0*{y_B}_0),(x_1,{y_A}_1*{y_B}_1),...,(x_n,{y_A}_n*{y_B}_n))$
• 把系数表示法变为点值表示法的运算叫做点值运算，
• 把点值表示法变为系数表示法的运算叫做插值运算，
• 这两种运算是互逆的，同时也一定是可逆的。
• 仿佛发现什么不可告人的秘密（难道就这么简单？）
• 按这样的步骤相乘不就是 $O(n)$的了？
• 没错，相乘是 $O(n)$的，但做点值和插值运算呢？还是 $O(n^2)$的~~~
• 这两个运算的朴素过程分别被称为DFT（离散傅里叶变换）和IDFT（离散傅里叶逆变换）。
• 如何加速？

突破

• 傅里叶想到了要用单位根，
• 若 $x^n=1$，则 $x$为 $n$次单位根，
• 那我们先想想，
• 实数范围内， $1^2={-1}^2=1$，
• 推广到虚数， $1^4={-1}^4=i^4={-i}^4=1$，那也才 $4$个 $x$，远远不够。
• 那我们不如把实数和虚数结合吧，也就是复数！（高中会学）

为什么

关于复数

• 它的形如 $a+bi$的一个数，且 $a,b\in R$， $a$为实部， $b$为虚部，

• 关于它们的运算：

• $(a+bi)+(c+di)=(a+c)+(b+d)i$

• $(a+bi)-(c+di)=(a-c)+(b-d)i$

• $(a+bi)*(c+di)=a*c+a*di+bi*c+bi*di=ac+(ad+bc)i+bd(i^2)=(ac-bd)+(ad+bc)i$

• $\frac{a+bi}{c+di}=\frac{(a+bi)(c+di)}{(c+di)(c-di)}=\frac{(ac-bd)+(ad+bc)i}{c^2+d^2}$

• （除法可以不用管）

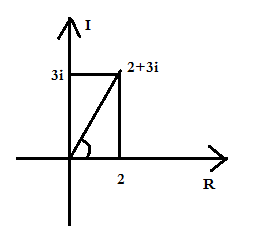
• 复数可以放在一个坐标系（复平面直角坐标系）中表示，

• 对于复数 $a+bi$，在坐标系中的坐标为 $(a,b)$，

• 

• 点到原点的线段称为模，模与 $R$轴（实数轴）正半轴的夹角称为幅角，

• 将复数乘法放在坐标系中，那么答案的位置就是相乘的两数模长相乘，幅角相加，

• 那么以原点为圆心， $1$个单位长度为半径作圆，得到圆称为单位圆，

• 将圆从 $(1,0)$开始 $n$等分，第二个点为 $w_n^1$，就是 $n$次单位根，坐标为 $(cos(\frac{2\pi}{n}),sin(\frac{2\pi}{n}))$

• 则根据乘法在坐标系上的法则，可以得到每个点的表示的复数分别为 $w_n^0,w_n^1..w_n^{n-1}$，（ $w_n^0=w_n^n)$

• $w_n^i$坐标为 $(cos(\frac{2\pi}{n}*i),sin(\frac{2\pi}{n}*i))$， $\pi$是按弧度制的等于 $180\degree$
  

• （如 $n=3$）

• 它们都可以满足 $(w_n^i)^n=1$，

• 首先，模长无论乘多少次都是 $1$，

• 其次， $w_n^i$的幅角的 $n$倍为 $\frac{360\degree}{n}*i*n=360\degree*i$，也就是绕着原点转了 $i$圈，回到 $x$轴正半轴，

• 因此得证。

• 接下来要看单位根的一些性质，

• 一、 $w_{dn}^{di}=w_n^i$

• 证明：

• $w_{dn}^{di}=cos(\frac{2\pi}{dn}*di)+sin(\frac{2\pi}{dn}*di)*i=cos(\frac{2\pi}{n}*i)+sin(\frac{2\pi}{n}*i)*i=w_n^i$

• 二、 $w_n^k=-w_n^{k+\frac{n}{2}}$

• 相当于将这个点旋转 $180\degree$，则到了与它关于原点对称的位置,

• 证明：

• $w_n^{\frac{n}{2}}=cos(\frac{2\pi}{n}*\frac{n}{2})+sin(\frac{2\pi}{n}*\frac{n}{2})*i=cos(\pi)+sin(\pi)*i=-1$

• $w_n^k=-w_n^k*(-1)=-w_n^k*w_n^\frac{n}{2}=-w_n^{k+\frac{n}{2}}$

FFT

• 终于可以进入正题了（铺垫实在是太多了）！！！
• 既然我们得出了单位根，那它一定能发挥一定作用，
• 根据上面的一些性质，DFT可以用分治来完成，时间复杂度优化到 $O(n\log_2 n)$.
• 设 $n$项式 $A(x)$，
• $A(x)=\sum_{i=0}^{n-1}a_i*x^i=a_n*x^n+a_{n-1}*x^{n-1}+...+a_1*x+a_0$
• 把偶数次项和奇数次项分开，
• $A(x)=(a_{n-2}*x^{n-2}+a_{n-4}*x^{n-4}+...+a_2*x^2+a0)+(a_{n-1}*x^{n-1}+a_{n-3}*x^{n-3}+...+a_3*x^3+a_1*x)$
• $=(a_{n-2}*x^{n-2}+a_{n-4}*x^{n-4}+...+a_2*x^2+a0)+x*(a_{n-1}*x^{n-2}+a_{n-3}*x^{n-4}+...+a_3*x^2+a_1)$
• 发现两边括号内每一项的指数已经相等了，那么再设
• $A_0(x)=a_{n-2}*x^{n-1}+a_{n-4}*x^{n-2}+...+a_2*x+a0$
• $A_1(x)=a_{n-1}*x^{n-1}+a_{n-3}*x^{n-2}+...+a_3*x+a_1$
• （注意指数与 $a$的下标不是相等的了，而是变成了 $\frac{1}{2}$）
• 于是可以得到，
• $A(x)=A_0(x^2)+x*A_1(x^2)$
• 对于代入的 $w_n^k(k<\frac{n}{2})$分两种情况，有
• $A(w_n^k)$
• $=A_0((w_n^k)^2)+w_n^k*A_1((w_n^k)^2)$
• $=A_0(w_n^{2k})+w_n^k*A_1(w_n^{2k})$
• $=A_0(w_{\frac{n}{2}}^k)+w_n^k*A_1(w_{\frac{n}{2}}^k)$
• $A(w_n^{k+\frac{n}{2}})$
• $=A_0((w_n^{k+\frac{n}{2}})^2)+w_n^{k+\frac{n}{2}}*A_1((w_n^{k+\frac{n}{2}})^2)$
• $=A_0(w_n^{2k+n})+w_n^{k+\frac{n}{2}}*A_1(w_n^{2*k+n})$
• $=A_0(w_n^n*w_n^{2k})+w_n^{k+\frac{n}{2}}*A_1(w_n^n*w_n^{2k})$
• $=A_0(w_{\frac{n}{2}}^k)-w_n^k*A_1(w_{\frac{n}{2}}^k)$
• 因此，我们知道了 $A_0(x)$和 $A_1(x)$分别在 $(w_{\frac{n}{2}}^0,w_{\frac{n}{2}}^1,...,w_{\frac{n}{2}}^{\frac{n}{2}-1})$的点值表示，就可以算出 $A(x)$在 $(w_n^0,w_0^1,...,w_n^{n-1})$的点值表示了。
• 显然这就是一个分治的过程，边界为 $n=1$
• 记得在做之前把 $n$补到 $2$的幂数，多出部分的系数就全都为 $0$，.
• 点值运算完成后，再根据上面的【关于多项式】和【为什么】的内容，就可以得出最终的答案了，
• 务必记得最终的多项式系数要全部除以 $n$.
• 这样一来，时间就可以优化到 $O(n \log n)$.

板子（洛谷3809过不去的）

#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
#define ld long double
#define N 2000010
const ld pi=acos(-1.0);
ld read()
{
	ld s=0;
	int x=getchar();
	while(x<'0'||x>'9') x=getchar();
	while(x>='0'&&x<='9') s=s*10+x-'0',x=getchar();
	return s;
}
struct node
{
	ld x,y;
	node(ld xx=0,ld yy=0) 
	{
		x=xx,y=yy;
	}
}a[N],b[N];
node operator +(node x,node y) 
{
	return node{x.x+y.x,x.y+y.y};
}
node operator -(node x,node y) 
{
	return node{x.x-y.x,x.y-y.y};
}
node operator *(node x,node y)
{
	return node(x.x*y.x-x.y*y.y,x.x*y.y+x.y*y.x);
}
void FFT(int len,node *a,int p)
{
	if(len==1) return;
	node a0[len/2+3],a1[len/2+3];
	for(int i=0;i<=len;i+=2) a0[i/2]=a[i],a1[i/2]=a[i+1];
	FFT(len/2,a0,p);
	FFT(len/2,a1,p);
	node w=node(cos(2*pi/len),p*sin(2*pi/len));
	node w0=node(1,0);
	for(int i=0;i<len/2;i++)
	{
		a[i]=a0[i]+w0*a1[i];
		a[i+len/2]=a0[i]-w0*a1[i];
		w0=w0*w;
	}
}
int main()
{
	int n,m,i;
	n=read(),m=read();
	for(i=0;i<=n;i++) a[i].x=read();
	for(i=0;i<=m;i++) b[i].x=read();
	int len=1;
	for(;len<=n+m;len*=2);
	FFT(len,a,1);
	FFT(len,b,1);
	for(i=0;i<=len;i++) a[i]=a[i]*b[i];
	FFT(len,a,-1);
	for(i=0;i<=n+m;i++) printf("%.0Lf ",a[i].x/len+1e-6);
	return 0;
}

原因

• 常数大。。。

解决办法

• 优化！

优化

• 原来的做法是先分别读入 $a,b$的实部（因为它们没有虚部），然后分别做点值运算，相乘后做插值运算。
• 现在把 $b$的实部直接作为 $a$的虚部，设改变之后的系数分别为 $c_i$，
• 那么 $c_i=a_i+b_i*i$，
• 有 $c^2=a^2-b^2+2abi$，那么虚部的 $2ab$在原先必须除以 $n$的基础上再多除以 $2$就是答案。
• 所以时间可以优化。

真·优化

• 想办法把 $DFS$去掉。
• 设原序列 $(A_0,A_1,A_2,A_3,A_4,A_5,A_6,A_7,A_8,A_9,A_{10},A_{11},A_{12},A_{13},A_{14},A_{15})$，
• 分治每次变换后：
• $(A_0,A_2,A_4,A_6,A_8,A_{10},A_{12},A_{14})，(A_1,A_3,A_5,A_7,A_9,A_{11},A_{13},A_{15})$
• $(A_0,A_4,A_8,A_{12})，(A_2,A_6,A_{10},A_{14})，(A_1,A_5,A_9,A_{13})，(A_3,A_7,A_{11},A_{15})$
• $(A_0,A_8)，(A_4,A_{12})，(A_2,A_{10})，(A_6,A_{14})，(A_1,A_9)，(A_5,A_{13})，(A_3,A_{11})，(A_7,A_{15})$
• 到每组连个数时，把它们的下标和所在位置排列起来：
• $(0,8,4,12,2,10,6,14,1,9,5,13,3,11,7,15)$
• $(0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15)$
• 它们对应的二进制是：
• $(0000,1000,0100,1100,0010,1010,0110,1110,0001,1001,0101,1101,0011,1011,0111,1111)$
• $(0000,0001,0010,0011,0100,0101,0110,0111,1000,1001,1010,1011,1100,1101,1110,1111)$
• 发现对应的每一位都是相反的，
• 那就根据这个把最终的序列求出来，再一步步反推回去。
• 以上被称为蝴蝶变换。

真·板子

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
#define ld double
#define N 8000010
#define pi M_PI
ld read()
{
	ld s=0;
	int x=getchar();
	while(x<'0'||x>'9') x=getchar();
	while(x>='0'&&x<='9') s=s*10+x-'0',x=getchar();
	return s;
}
struct node
{
	ld x,y;
	node(ld xx=0,ld yy=0) 
	{
		x=xx,y=yy;
	}
}a[N];
int rev[N];
node operator +(node x,node y) 
{
	return node{x.x+y.x,x.y+y.y};
}
node operator -(node x,node y) 
{
	return node{x.x-y.x,x.y-y.y};
}
node operator *(node x,node y)
{
	return node(x.x*y.x-x.y*y.y,x.x*y.y+x.y*y.x);
}
void FFT(int len,ld p)
{
	for(int i=0;i<len;i++) if(i<rev[i]) swap(a[i],a[rev[i]]);
	for(int i=1;i<len;i*=2)
	{
		node w=node(cos(pi/i),p*sin(pi/i));
		for(int j=0;j<len;j+=2*i)
		{
			node w0=node(1,0);
			for(int k=0;k<i;k++)
			{
				node A=a[k+j],B=a[k+j+i];
				a[k+j]=A+B*w0;
				a[k+j+i]=A-B*w0;
				w0=w0*w;
			}
		}
	}
}
int main()
{
	int n,m,i;
	n=read(),m=read();
	for(i=0;i<=n;i++) a[i].x=read();
	for(i=0;i<=m;i++) a[i].y=read();
	int len=1,ls=0;
	for(;len<=n+m;len*=2,ls++);
	for(i=0;i<len;i++) 
	{
		int t=i;
		for(j=1;j<=ls;j++) rev[i]=rev[i]*2+t%2,t/=2;
	}
	FFT(len,1);
	for(i=0;i<=len;i++) a[i]=a[i]*a[i];
	FFT(len,-1);
	for(i=0;i<=n+m;i++) printf("%.0lf ",a[i].y/2/len+1e-3);
	return 0;
}